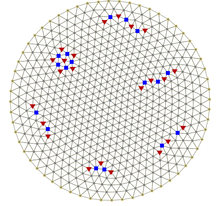
- Wigner crystal
-
A Wigner crystal is the solid (crystalline) phase of electrons first predicted by Eugene Wigner in 1934.[1] A gas of electrons moving in 2D or 3D in a uniform, inert, neutralizing background will crystallize and form a lattice if the electron density is less than a critical value. This is because the potential energy dominates the kinetic energy at low densities, so the detailed spatial arrangement of the electrons becomes important. To minimize the potential energy, the electrons form a b.c.c. (body-centered cubic) lattice in 3D, a triangular lattice in 2D and a evenly spaced lattice in 1D. Most experimentally observed Wigner clusters exist due to the presence of the external confinement, i.e. external potential trap. As a consequence, deviations from the b.c.c or triangular lattice are observed [2]. A crystalline state of the 2D electron gas can also be realized by applying a sufficiently strong magnetic field. However, it is still not clear whether it is the Wigner-crystalization that has led to observation of insulating behaviours in magnetotransport measurements on 2D electron systems, since other candidates are present, such as Anderson localization.[clarification needed]
There is a single dimensionless parameter characterising the state of a uniform electron gas at zero temperature, the so-called Wigner-Seitz radius rs = a / ab, where a is the average inter-particle spacing and ab is the Bohr radius. Quantum Monte Carlo simulations indicate that the uniform electron gas crystallizes at rs = 106 in 3D[3][4] and roughly rs = 35 in 2D.[5][6]
For classical systems at elevated temperatures one uses the average interparticle interaction in units of the temperature: G = e2 / (kB Ta). The Wigner transition occurs at G = 170 in 3D[7] and G = 125 in 2D.[8] It is believed that ions, such as those of iron, form a Wigner crystal in the interiors of white dwarf stars.
More generally, a Wigner crystal phase can also refer to a crystal phase occurring in non-electronic systems at low density. In contrast, most crystals melt as the density is lowered. Examples seen in the laboratory are charged colloids or charged plastic spheres.
In practice, it is difficult to experimentally realize a Wigner crystal because quantum mechanical fluctuations overpower the Coulomb repulsion and quickly cause disorder. Low electron density is needed. One notable example occurs in quantum dots with low electron densities or high magnetic fields where electrons will spontaneously localize in some situations, forming a so-called rotating "Wigner molecule",[9] a crystalline-like state adapted to the finite size of the quantum dot.
Another experimental realisation of the Wigner crystal occurs in single electron transistors with very low currents, where a 1D Wigner crystal will form. The current due to each electron can be directly detected experimentally.[10]
References
- ^ Wigner, E. (1934). "On the Interaction of Electrons in Metals". Physical Review 46: 1002. Bibcode 1934PhRv...46.1002W. doi:10.1103/PhysRev.46.1002.
- ^ Radzvilavicius, A.; Anisimovas, E. (2011). "Topological defect motifs in two-dimensional Coulomb clusters". J. Phys.: Condens. Matter 23: 385301. Bibcode 2011JPCM...23L5301R. doi:10.1088/0953-8984/23/38/385301.
- ^ Ceperley, D. M. (1980). "Ground State of the Electron Gas by a Stochastic Method". Physical Review Letters 45: 566. Bibcode 1980PhRvL..45..566C. doi:10.1103/PhysRevLett.45.566.
- ^ Drummond, N.; Radnai, Z.; Trail, J.; Towler, M.; Needs, R. (2004). "Diffusion quantum Monte Carlo study of three-dimensional Wigner crystals". Physical Review B 69: 085116. Bibcode 2004PhRvB..69h5116D. doi:10.1103/PhysRevB.69.085116.
- ^ Tanatar, B.; Ceperley, D. (1989). "Ground state of the two-dimensional electron gas". Physical Review B 39: 5005. Bibcode 1989PhRvB..39.5005T. doi:10.1103/PhysRevB.39.5005.
- ^ Rapisarda, F.; Senatore, G. (1996). "Diffusion Monte Carlo study of electrons in two-dimensional layers". Australian Journal of Physics 49: 161. Bibcode 1996AuJPh..49..161R.
- ^ Dubin, D. H. E.; O'neil, T. M. (1999). "Trapped nonneutral plasmas, liquids, and crystals (the thermal equilibrium states)". Reviews of Modern Physics 71: 87. Bibcode 1999RvMP...71...87D. doi:10.1103/RevModPhys.71.87.
- ^ Imai, Y.; Kawakami, N.; Tsunetsugu, H. (2003). "Low-energy excitations of the Hubbard model on the Kagomé lattice". Physical Review B 68: 195103. arXiv:cond-mat/0305144. Bibcode 2003PhRvB..68s5103I. doi:10.1103/PhysRevB.68.195103.
- ^ Yannouleas, C.; Landman, U. (2007). "Symmetry breaking and quantum correlations in finite systems: studies of quantum dots and ultracold Bose gases and related nuclear and chemical methods". Reports on Progress in Physics 70: 2067. Bibcode 2007RPPh...70.2067Y. doi:10.1088/0034-4885/70/12/R02.
- ^ "Current measurement by real-time counting of single electrons". Nature 434: 361−364. 2005. arXiv:cond-mat/0411420. Bibcode 2005Natur.434..361B. doi:10.1038/nature03375. http://www.nature.com/doifinder/10.1038%2Fnature03375. (see also the Nature review article here
Categories:
Wikimedia Foundation. 2010.