Mixed boundary condition

Green: Neumann boundary condition; purple: Dirichlet boundary condition.

In mathematics, a mixed boundary condition for a partial differential equation indicates that different boundary conditions are used on different parts of the boundary of the domain of the equation.

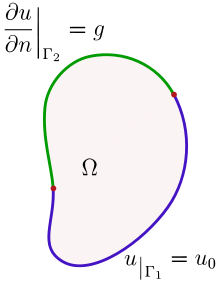
For example, if u is a solution to a partial differential equation on a set Ω with piecewise-smooth boundary $\partial\Omega$, and $\partial\Omega$ is divided into two parts, Γ₁ and Γ₂, one can use a Dirichlet boundary condition on Γ₁ and a Neumann boundary condition on Γ₂:

$u_{\big| \Gamma_1} = u_0$

$\left. \frac{\partial u}{\partial n}\right|_{\Gamma_2} = g$

where u₀ and g are given functions defined on those portions of the boundary.

Robin boundary condition is another type of hybrid boundary condition; it is a linear combination of Dirichlet and Neumann boundary conditions.

See also

• Dirichlet boundary condition
• Neumann boundary condition
• Cauchy boundary condition
• Robin boundary condition

References

• Guru, Bhag S.; Hiziroglu, Hüseyin R. (2004). Electromagnetic field theory fundamentals, 2nd ed.. Cambridge, UK; New York: Cambridge University Press. p. 593. ISBN 0521830168. 

This applied mathematics-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Applied mathematics stubs Boundary conditions Partial differential equations Wikimedia Foundation. 2010. Игры ⚽ Нужна курсовая? Budhi Gandak Weihai dialect Look at other dictionaries: Robin boundary condition — In mathematics, the Robin (or third type) boundary condition is a type of boundary condition, named after Victor Gustave Robin (1855 1897) who lectured in mathematical physics at the Sorbonne in Paris and worked in the area of thermodynamics.… …   Wikipedia Dirichlet boundary condition — In mathematics, the Dirichlet (or first type) boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet (1805–1859) who studied under Cauchy and succeeded Gauss at University of Göttingen.[1] When… …   Wikipedia Neumann boundary condition — In mathematics, the Neumann (or second type) boundary condition is a type of boundary condition, named after Carl Neumann.[1] When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a… …   Wikipedia Cauchy boundary condition — In mathematics, a Cauchy (pronounced koe she ) boundary condition imposed on an ordinary differential equation or a partial differential equation specifies both the values a solution of a differential equation is to take on the boundary of the… …   Wikipedia Planetary boundary layer — Depiction of where the planetary boundary layer lies on a sunny day The planetary boundary layer (PBL), also known as the atmospheric boundary layer (ABL), is the lowest part of the atmosphere and its behavior is directly influenced by its… …   Wikipedia Spectral theory of ordinary differential equations — In mathematics, the spectral theory of ordinary differential equations is concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation Hermann Weyl… …   Wikipedia List of mathematics articles (M) — NOTOC M M estimator M group M matrix M separation M set M. C. Escher s legacy M. Riesz extension theorem M/M/1 model Maass wave form Mac Lane s planarity criterion Macaulay brackets Macbeath surface MacCormack method Macdonald polynomial Machin… …   Wikipedia Partial differential equation — A visualisation of a solution to the heat equation on a two dimensional plane In mathematics, partial differential equations (PDE) are a type of differential equation, i.e., a relation involving an unknown function (or functions) of several… …   Wikipedia D-brane — String theory Superstring theory …   Wikipedia Airy wave theory — In fluid dynamics, Airy wave theory (often referred to as linear wave theory) gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform… …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”