Axiom (computer algebra system)

"Scratchpad" redirects here. For scratchpad memory, see Scratchpad RAM.

Axiom

Developer(s)	independent group of people
Stable release	September 2011
Operating system	cross-platform
Type	computer algebra system
License	Modified BSD License
Website	axiom-developer.org

Axiom is a free, general-purpose computer algebra system. It consists of an interpreter environment, a compiler and a library, which defines a strongly typed, mathematically (mostly) correct type hierarchy.

History

Axiom has been in development since 1971,^[1] originally as Scratchpad by researchers at IBM under the direction of Richard Dimick Jenks.^[2] Other key early developers were Barry Trager, Stephen Watt, James Davenport, Robert Sutor, and Scott Morrison.

In the 1990s it was sold to NAG and given its current name. In 2001 it was withdrawn from the market and re-released under the Modified BSD License. Since then, the project lead developer has been Tim Daly.

In 2007, Axiom was forked into two different open-source projects: OpenAxiom,^[3] and FriCAS.^[4]

Documentation

Axiom is a literate program. The source code is becoming available in a set of volumes which are available on the axiom-developer.org^[5] website. These volumes contain the actual source code of the system.

The currently available documents are:

• Combined Table of Contents
• Volume 0: Axiom Jenks and Sutor -- The main textbook
• Volume 1: Axiom Tutorial -- A simple introduction
• Volume 2: Axiom Users Guide -- Detailed examples of domain use (incomplete)
• Volume 3: Axiom Programmers Guide -- Guided examples of program writing (incomplete)
• Volume 4: Axiom Developers Guide -- Short essays on developer-specific topics (incomplete)
• Volume 5: Axiom Interpreter -- Source code for Axiom interpreter (incomplete)
• Volume 6: Axiom Command -- Source code for system commands and scripts (incomplete)
• Volume 7: Axiom Hyperdoc -- Source code and explanation of X11 Hyperdoc help browser
  • Volume 7.1 Axiom Hyperdoc Pages -- Source code for Hyperdoc pages
• Volume 8: Axiom Graphics -- Source code for X11 Graphics subsystem
• Volume 9: Axiom Compiler -- Source code for Spad compiler (incomplete)
• Volume 10: Axiom Algebra Implementation -- Essays on implementation issues (incomplete)
  • Volume 10.1: Axiom Algebra Theory -- Essays containing background theory
  • Volume 10.2: Axiom Algebra Categories -- Source code for Axiom categories
  • Volume 10.3: Axiom Algebra Domains -- Source code for Axiom domains
  • Volume 10.4: Axiom Algebra Packages -- Source code for Axiom packages
  • Volume 10.5: Axiom Algebra Numerics -- Source code for Axiom numerics
• Volume 11: Axiom Browser -- Source pages for Axiom Firefox browser front end
• Volume 12: Axiom Crystal -- Source code for Axiom Crystal front end (incomplete)
• Bibliography: Axiom Bibliography -- Literature references

Videos

The Axiom project has a major focus on providing documentation. Recently the project announced the first in a series of instructional videos, which are also available on the axiom-developer.org^[6] website. The first video^[7] provides details on the Axiom information sources.^[8]

Philosophy

The Axiom project focuses on the “30 Year Horizon”. The primary philosophy is that Axiom needs to develop several fundamental features in order to be useful to the next generation of computational mathematicians. Knuth's literate programming technique is used throughout the source code. Axiom plans to use proof technology to prove the correctness of the algorithms (such as Coq and ACL2).

Design

In Axiom, all objects have a type. Examples of types are mathematical structures (such as rings, fields, polynomials) as well as data structures from computer science (e.g., lists, trees, hash tables).

A function can take a type as argument, and its return value can also be a type. For example, Fraction is a function, that takes an IntegralDomain as argument, and returns the field of fractions of its argument. As another example, the ring of $4\times 4$ matrices with rational entries would be constructed as SquareMatrix(4, Fraction Integer). Of course, when working in this domain, 1 is interpreted as the identity matrix and A^-1 would give the inverse of the matrix A, if it exists.

Several operations can have the same name, and the types of both the arguments and the result are used to determine which operation is applied (cf. function overloading).

Axiom comes with an extension language called SPAD. All the mathematical knowledge of Axiom is written in this language. The interpreter accepts roughly the same language. SPAD was further developed under the name A# and later Aldor. The latter can still be used as an alternative extension language. It is, however, distributed under a different license.

Features

Within the interpreter environment, Axiom uses type inference and a heuristic algorithm to make explicit type annotations mostly unnecessary.

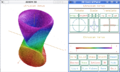
It features 'HyperDoc', an interactive browser-like help system, and can display two and three dimensional graphics, also providing interactive features like rotation and lighting. It also has a specialised interaction mode for Emacs, as well as a plugin for the TeXmacs editor.

• 

  HyperDoc displaying the available operations for a domain

• 

  Axiom displaying a surface

• 

  Axiom Firefox Browser Interface

• 

  Axiom simplifying a heat equation

• 

  Axiom matrix manipulation

• 

  Axiom computing a Risch integral

Axiom has an implementation of the Risch algorithm for elementary integration, which was done by Manuel Bronstein and Barry Trager.

See also

Free software portal

• A# programming language
• Aldor programming language
• Comparison of computer algebra systems

References

1. ^ Axiom Homepage
2. ^ CIS.udel.edu
3. ^ Open-axiom.org
4. ^ fricas.sourceforge.net
5. ^ Axiom-developer.org
6. ^ Axiom-developer.org
7. ^ Youtube.com
8. ^ "Axiom Computer Algebra System Information Sources," jgg899, YouTube, November 30, 2008.

• J. H. Griesmer and R.D.Jenks "SCRATCHPAD/1 -- an interactive facility for symbolic mathematics"
• R. D. Jenks "META/PLUS The Syntax Extension Facility for SCRATCHPAD" Research Report RC 3259 IBM T.J.Watson Research Center, Yorktown Heights, N.Y. (1971)
• J. Griesmer and R. Jenks "Experience with an online symbolic math. system SCRATCHPAD" (1972) PKI-OG: Li-Ord.Le
• James H. Griesmer and Richard D. Jenks "SCRATCHPAD: A capsule view" SIGPLAN v7 n10 pp 93–102 (1972)
• R. D. Jenks "The SCRATCHPAD Language" SIGPLAN v9 n4 pp101–111 (1974) ISSN 0362-1340
• A. C. Norman "Computing with Formal Power Series" TOMS v1 n4 pp346–356 (1975) ISSN 0098-3500
• Richard D. Jenks "A pattern compiler" Symsac '76 pp60–65 (1976)
• E. Lueken "Ueberlegungen zur Implementierung eines Formelmanipulationssystems" Masters Thesis Technischen Universitat Carolo-Wilhelmina zu Braunschweig, Germany (1977)
• George E. Andrews "Ramanugan and SCRATCHPAD" p303-?? (1984)
• J. Davenport, P. Gianni, R. Jenks, V. Miller, S. Morrison, M. Rothstein, C. Sundaresan, R. Sutor, B. Trager "Scratchpad" Mathematical Sciences Department IBM Thomas Watson Research Center (1984)
• Richard D. Jenks "The New SCRATCHPAD Language and System for Computer Algebra" pp409-??
• Richard D. Jenks "A primer: 11 keys to New Scratchad" pp123–147 (1984)
• R. S. Sutor "The Scratchpad II Computer Algebra Language and System" pp32–33 (1985)
• Rudiger Gebauer and H. Michael Moller "Buchberger's algorithm and staggered linear bases" SYMSAC '86 (1986) ACM pp218–221 ISBN 0-89791-199-7
• Richard D. Jenks, Robert S. Sutor, Stephen M. Watt "Scratchpad II: an abstract datatype system for mathematical computation" Research Report RC12327 IBM T.J.Watson Research Center (1986)
• Michael Lucks and Bruce W. Char "A fast implementation of polynomial factorization" SYMSAC '86 (1986) ACM ISBN 0-89791-199-7 pp228–232
• J. Purtilo "Applications of a software interconnection system in mathematical problem solving environments" SYMSAC '86 (1986) ACM ISBN 0-89791-199-7 pp16–23
• W. Burge and S. Watt "Infinite Structure in SCRATCHPAD II" FC 12794 IBM T.J.Watson Research Center (1987)
• P. Senechaud, F. Siebert, G. Villard "Scratchpad II: Presentation d'un nouveau langage de calcul formel" TIM 3 (IMAG) Grenoble, France (1987)
• R. S. Sutor and R.D.Jenks "The Type Inference and Coercion Facilities in the Scratchpad II Interpreter" Wexelblat:1987:IIT pp56–63 (1987)
• Robert S. Sutor and Richard D. Jenks "The type inference and coercion facilities in the Scratchpad II interpreter" Research Report RC 12595 IBM T.J.Watson Research Center (1987)
• G. E. Andrews "Application of Scratchpad to problems in special functions and combinatorics" pp158-?? (1988)
• J. H. Davenport, Y.Siret, E.Tournier "Computer Algebra: Systems and Algorithms for Algebraic Computation" ISBN 0-12-204230-1 (1995)
• R. Gebauer and H.M.Moller "On an installation of Buchberger's algorithm" Journal of Symbolic Computation v6 n2-3 pp275–286 (1988) ISSN 07470-7171
• F. Schwarz "Programming with abstract data types: the symmetry package (SPDE) in Scratchpad Janssen:1988:TCA pp167-176 (1988)
• D. Shannon and M.Sweedler "Using Groebner bases to determine algebra membership, split surjective algebra homomorphisms determine birational equivalence" Journal of Symbolic Computation v6 n2-3 pp267–273 (1988)
• Hans-J. Boehm "Type inference in the presence of type abstraction" SIGPLAN v24 n7 pp192–206 (1989)
• Bronstein, M. "Simplification of real elementary functions" ACM:1989:PAI pp207–211 (1989)
• C. Dicrescenzo and D. Duval "Algebraic extensions and algebraic closure in Scratchpad II" Gianni:1989:SAC pp440–446 (1989)
• Daly, Timothy "Axiom -- Thirty Years of Lisp"
• Daly, Timothy Axiom Invited Talk, Free Software Conference, Lyon, France, May, 2002
• Daly, Timothy Software Meeting Axiom Invited Talk Metz, France, July 9–12, 2003

External links

• Axiom Homepage
• Homepage hosting all descendents of the original project
• Jenks, R.D. and Sutor, R. "Axiom, The Scientific Computation System"
• Daly, T. "Axiom Volume 1: Tutorial"

Software forks:

• OpenAxiom website. OpenAxiom SourceForge.net project page.
• FriCAS website. FriCAS SourceForge.net project page.