Miwin's dice

Miwin's Dice

Miwin's Dice made of titanium
Designer(s)	Dr. Michael Winkelmann
Publisher(s)	Arquus Verlag Vienna
Years active	1994
Players	1–9
Age range	6+, depending on game
Playing time	5–60 minutes, depending on game
Website	www.miwin.com

Miwin's Dice are a set of nontransitive dice invented in 1975 by the physicist Michael Winkelmann. They consist of three different dice with faces bearing numbers from 1 to 9; opposite faces sum to 9, 10, or 11. The numbers on each die give the sum of 30 and have an arithmetic mean of 5.

Description

Miwins dice IX, X, XI

Miwin's dice have 6 sides, each of which bear a number, depicted in a pattern of dots. The standard set is made of wood; special designs are made of titanium or other materials (gold, silver).

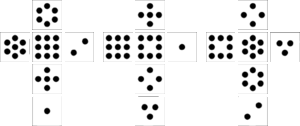
First set of Miwin's dice: III, IV, V

design of numbers of Miwins dice III, IV, V

Each die is named for the sum of its 2 lowest numbers. The dots on each die are colored blue, red or black. Each die has the following numbers:

Die III	with blue dots	1	2			5	6	7		9
Die IV	with red dots	1		3	4	5			8	9
Die V	with black dots		2	3	4		6	7	8

Numbers 1 and 9, 2 and 7, and 3 and 8 are on opposite sides on all three dice. Additional numbers are 5 and 6 on die III, 4 and 5 on die IV, and 4 and 6 on die V. The dice are designed in such a way that, for every die, another will usually win against it. The probability that a given die will have a higher number than another is 17/36; a lower number, 15/36. Thus, die III wins against IV, IV against V, and V against III. Such dice are known as nontransitive.

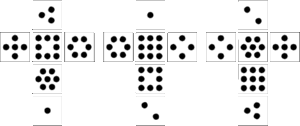
Second set of Miwin's dice: IX, X, XI

design of numbers of Miwins dice IX, X, XI

Each die is named for the sum of its lowest and highest numbers. The dots on each die are colored yellow, white or green. Each die has the following numbers:

Die IX	with yellow dots	1		3		5	6	7	8
Die X	with white dots	1	2		4		6		8	9
Die XI	with green dots		2	3	4	5		7		9

Mathematical attributes

Each of the dice has similar attributes: each die bears each of its numbers exactly once, the sum of the numbers is 30, and each number from 1 to 9 is spread twice over the three dice. This attribute characterizes the implementation of intransitive dice, enabling the different game variants. All the games need only 3 dice, in comparison to other theoretical nontransitive dice, designed in view of mathematics, such as Efron's dice.^[1]

Because of these special attributes, Miwin's dice are also used in education. Miwin's dice help to develop mathematical thinking and enhance the ability to calculate probability, as was demonstrated during a seminar at the University of Siegen in the Summer of 2007.^{[citation needed]}

Probabilities

• 1/3 of the sum of dots of all dice can be divided by 3 without carry over.
• 1/3 of the sum of dots of all dice can be divided by 3 having a carry over of 1.
• 1/3 of the sum of dots of all dice can be divided by 3 having a carry over of 2.

The probability for a given number with all 3 dice is 11/36, for a given rolled double is 1/36, for any rolled double 1/4. The probability to obtain a rolled double is only 50% compared to normal dice.

Cumulative frequency

• 

  Cumulative frequency type III and IV

• 

  Cumulative frequency type III and V

• 

  Cumulative frequency type IV and V

• 

  Cumulative frequency type III and IV and V = "Miwin-Distribution"

Reversed intransitivity

Removing the common dots of Miwin's Dice reverses intransitivity.^{[citation needed]}

Die III	with blue dots	1	2			5	6	7		9	→ Die III'	2	6	7
Die IV	with red dots	1		3	4	5			8	9	→ Die IV'	3	4	8

III:IV = 17:16, III':IV' = 4:5   →   IV' > III'
analog: III/V, IV/V

Equal distribution of random numbers

Miwin's dice facilitate generating numbers at random, within a given range, such that each included number is equally-likely to occur. In order to obtain a range that does not begin with 1 or 0, simply add a constant value to bring it into that range (to obtain random numbers between 8 and 16, inclusive, follow the 1 – 9 instructions below, and add 7 to the result of each roll).

• 1 – 9: 1 die is rolled (chosen at random): P(1) = P(2) = ... = P(9) = 1/9

• 0 – 80: 2 dice are rolled (chosen at random), always subtract 1: P(0) = P(1) = ... = P(80) = 1/9² = 1/81

Other distributions

0 – 90 (throw 3 times)

Governing probability: P(0) = P(1) = ... = P(90) = 8/9³ = 8/729

To obtain an equal distribution with numbers from 0 – 90, all three dice are rolled, one at a time, in a random order. The result is calculated based on the following rules:

• 1st throw is 9, 3rd throw is not 9: gives 10 times 2nd throw (possible scores: 10, 20, 30, 40, 50, 60, 70, 80, 90)
• 1st throw is not 9: gives 10 times 1st throw, plus 2nd throw
• 1st throw is equal to the 3rd throw: gives 2nd throw (possible scores: 1, 2, 3, 4, 5, 6, 7, 8, 9)
• All dice equal: gives 0
• All dice 9: no score

Sample:

1st throw	2nd throw	3rd throw	Equation	Result
9	9	not 9	10 times 9	90
9	1	not 9	10 times 1	10
8	4	not 8	(10 times 8) + 4	84
1	3	not 1	(10 times 1) + 3	13
7	8	7	7 = 7, gives 8	8
4	4	4	all equal	0
9	9	9	all 9	-

This gives 91 numbers, from 0 – 90 with the probability of 8 / 9³, 8 × 91 = 728 = 9³ − 1

0 – 103 (throw 3 times)

Governing probability: P(0) = P(1) = ... = P(103) = 7/9³ = 7/729

This gives 104 numbers from 0 – 103 with the probability of 7 / 9³, 7 × 104 = 728 = 9³ − 1

0 – 728 (throw 3 times)

Governing probability: P(0) = P(1) = ... = P(728) = 1 / 9³ = 1 / 729

This gives 729 numbers, from 0 – 728, with the probability of 1 / 9³.

One die is rolled at a time, taken at random.

Create a number system of base 9:

• 1 must be subtracted from the face value of every roll because there are only 9 digits in this number system ( 0,1,2,3,4,5,6,7,8 )
• (1st throw) × 81 + (2nd throw) × 9 + (3rd throw) × 1

This system yields this maximum: 8 × 9² + 8 × 9 + 8 × 9° = 648 + 72 + 8 = 728 = 9³ − 1

Examples:

1st throw	2nd throw	3rd throw	Equation	Result
9	9	9	8 × 9² + 8 × 9 + 8	728
4	7	2	3 × 9² + 6 × 9 + 1	298
2	4	1	1 × 9² + 4 × 9 + 0	117
1	3	4	0 × 9² + 3 × 9 + 3	30
7	7	7	6 × 9² + 6 × 9 + 6	546
1	1	1	0 × 9² + 0 × 9 + 0	0
4	2	6	3 × 9² + 1 × 9 + 5	257

Combinations with Miwin's dice type III, IV, and V

Variant	Equation	number of variants
one throw with 3 dice, type is not used as attribute	-	135
one throw with 3 dice, type is an additional attribute	(135 – 6 × 9) × 2 + 54	216
1 throw with each type, type is not used as attribute	6 × 6 × 6	216
1 throw with each type, type is used as attribute	6 × 6 × 6 × 6	1296
3 throws, random selection of one of the dice for each throw, type is not used as attribute	9 × 9 × 9	729

3 throws, random selection of one of the dice for each throw, type is used as attribute:

Variant	Equation	number of alternatives
III, III, III / IV, IV, IV / V, V, V	3 × 6 × 6 × 6	648
III, III, IV / III, III, V / III, IV, IV / III, V, V / IV, IV, V / IV, V, V	6 × 3 × 216	+ 3888
III, IV, V / III, V, IV / IV, III, V / IV, V, III / V, III, IV / V, IV, III	6 × 216	+ 1296
		= 5832

5832 = 2 × 2 × 2 × 9 × 9 × 9 = 18³ numbers are possible.

Games

Since the middle of the 1980s, the press wrote about the games.^[2] Winkelmann presented games himself, for example, in 1987 in Vienna, at the "Österrechischen Spielefest, Stiftung Spielen in Österreich", Leopoldsdorf, where "Miwin's dice" won the prize "Novel Independent Dice Game of the Year".

In 1989, the games were reviewed by the periodical "Die Spielwiese".^[3] At that time, 14 alternatives of gambling and strategic games existed for Miwin's dice. The periodical "Spielbox" had two variants of games for Miwin's dice in the category "Unser Spiel im Heft" (now known as "Edition Spielbox"): the solitaire game 5 to 4, and the two-player strategic game Bitis.

In 1994, Vienna's Arquus publishing house published Winkelmann's book Göttliche Spiele,^[4] which contained 92 games, a master copy for 4 game boards, documentation about the mathematical attributes of the dice and a set of Miwin's dice. There are even more game variants listed on Winkelmann's website.^[5]

Solitaire games and games for up to nine players have been developed. Games are appropriate for players over 6 years of age. Some games require a game board; playing time varies from 5 to 60 minutes.

Variants 0 – 80

1st variant

Two dice are rolled, chosen at random, one at a time. Each pair is scored by multiplying the first by 9 and subtracting the second from the result: 1st throw × 9 − 2nd throw.

Examples:

1st throw	2nd throw	Equation	Result
9	9	9 × 9 − 9	72
9	1	9 × 9 − 1	80
1	9	9 × 1 − 9	0
2	9	9 × 2 − 9	9
2	8	9 × 2 − 8	10
8	4	9 × 8 − 4	68
1	3	9 × 1 − 3	6

This variant provides numbers from 0 – 80 with a probability of 1 / 9² = 1 / 81.

2nd variant

Two dice are rolled, chosen at random, one at a time. The pair is scored according to the following rules:

• 1st throw is 9: gives 10 × 2nd throw − 10
• 1st throw is not 9: gives 10 × 1st throw + 2nd throw − 10

Examples

1st throw	2nd throw	Equation	Result
9	9	10 × 9 − 10	80
9	1	10 × 1 − 10	0
8	4	10 × 8 + 4 − 10	74
1	3	10 × 1 + 3 − 10	3

This variant provides numbers from 0 – 80 with a probability of 1 / 9² = 1 / 81.

3rd variant

Two dice are rolled, chosen at random, one at a time. The score is obtained according to the following rules:

• Both throws are 9: gives 0
• 1st throw is 9 and 2nd throw is not 9: gives 10 × 2nd throw
• 1st throw is 8: gives 2nd throw
• All others: gives 10 × 1st throw − 2nd throw

Examples:

1st throw	2nd throw	Equation	Result
9	9	-	0
9	3	10 × 3	30
8	4	1 × 4	4
5	9	5 × 10 + 9	59

Notes

1. ^ http://www.miwin.com/ click "Miwin'sche Würfel 2", then check attributes
2. ^ Austrian paper "Das Weihnachtsorakel, Spieltip "Ein Buch mit zwei Seiten", the Standard 18.Dez..1994, page 6, Pöppel-Revue 1/1990 page 6 and Spielwiese 11/1990 page 13, 29/1994 page 7
3. ^ 29/1989 page 6
4. ^ The book on the German version of Amazon
5. ^ Winkelmann's homepage

External links

• Homepage of producer Michael Winkelmann
• Bitis in Ludings Game data base
• Game Tests

Published games

• Friedhelm Merz: Spiel ’89. Book for Gamblers, Game creators, Game producers and press. Merz Verl., Bonn 1989, ISBN 3-926108-23-1, S. 477.
• Michael Winkelmann: Göttliche Spiele Arquus-Verl. Pahlich 1994Göttliche Spiele Arquus-Verl. Pahlich 1994, ISBN 3-901-388-10-9,