Median voter theorem

One possible model; here, if parties A and B want to catch the median voters, they should move towards the center. The red and blue areas represent the voters that A and B expect they have already captured.

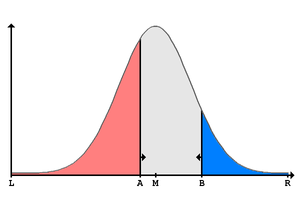
The median voter theory, also known as the median voter theorem or Black's theorem, is a famous voting theorem. It posits that in a majority election, if voter policy preferences can be represented as a point along a single dimension, if all voters vote deterministically for the politician who commits to a policy position closest to their own preference, and if there are only two politicians, then a politician maximizes their number of votes by committing to the policy position preferred by the median voter. This strategy is a Nash equilibrium. It results in voters being indifferent between the candidates and casting their votes for either candidate with equal probability. Hence, in expectation each politician receives half of the votes. If either candidate deviates to commit to a different policy position, the deviating candidate receives less than half the vote.

Political commentator Mickey Kaus of Slate Magazine wrote in 2004 that the United States presidential elections of 2000 and 2004, in addition to local elections in those years, provide evidence that this phenomenon is taking place in the United States.^[1]

The theorem was first articulated in Duncan Black's 1948 article, "On the Rationale of Group Decision-making"^[2] and popularized by Anthony Downs's 1957 book, An Economic Theory of Democracy.^[3] The theorem is central to moderation theory that delineates the processes through which radical political groups are incorporated into the existing political system.

Shortcomings of the Median Voter Model

There are many instances in which the Median Voter Theorem may not be applied. Among the most common is the case of preferences which are not single-peaked (multimodal preferences) or order-restricted. Consider the case where several voters are voting on the budget of a public school, for instance, and there are three options: low, medium and high. If one of the voters prefers both low and high to medium, then the preferences will not be single-peaked (they form a "valley", instead of a "mountain", if represented in a unidimensional diagram).

The non-verification of single-peaked preferences may lead to the Condorcet paradox, in which the agenda-maker who chooses in which order propositions are voted on may have the power to choose any outcome.^[4]

Generally, single-peaked preferences are a sufficient condition for the theorem to apply (Mas-Collel et al. 1995, pg. 802-3, Propositions 21.D.1 and 21.D.2). When preferences are not single-peaked or the policy space is multi-dimensional (e.g., individuals vote on both taxation and public expenditure), the median voter theorem yields no prediction. This has led some political economists to increasingly adopt the newer probabilistic voting theory, which has a unique equilibrium in a multi-dimensional spaces as well.^[4]

References

1. ^ Mickey Kaus (29 November 2004). "Fifty-Fifty Forever". Slate. http://www.slate.com/id/2073262/. Retrieved 18 September 2010. 
2. ^ Black, Duncan (1948). "On the rationale of group decision-making". Journal of Political Economy 56: 23–34. doi:10.1086/256633. 
3. ^ Downs, Anthony (1957). An Economic Theory of Democracy. Harper Collins. 
4. ^ ^{a b} McKelvey, R.D. (1976). "Intransitivities in multi dimensional voting models and some implications for agenda control". Journal of Economic Theory 12: 472–482. doi:10.1016/0022-0531(76)90040-5. 

• Mas-Colell, Andreu, Michael D. Whinston, and Jerry R. Green (1995). Microeconomic Theory. Oxford University Press. ISBN 978-0195073409. 
• Congleton, Roger (2002). The Median Voter Model. In * C. K. Rowley (Ed.); F. Schneider (Ed.) (2003). The Encyclopedia of Public Choice. Kluwer Academic Press. ISBN 978-0792386070. 

External links

Applications of median voter theory

• to tariffs
• to local private goods