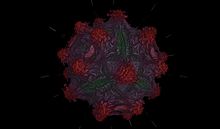
Mandelbulb

A ray-traced image of the 3D Mandelbulb
for the iteration z ↦ z⁸ + c.

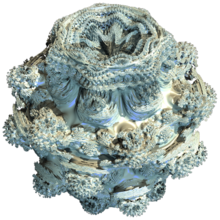
The Mandelbulb is a three-dimensional analogue of the Mandelbrot set, constructed by Daniel White and Paul Nylander using spherical coordinates.^[1]

A canonical 3-dimensional Mandelbrot set does not exist, since there is no 3-dimensional analogue of the 2-dimensional space of complex numbers. It is possible to construct Mandelbrot sets in 4 dimensions using quaternions. However, this set does not exhibit detail in all dimensions like the 2D Mandelbrot set.

White and Nylander's formula for the "nth power" of the 3D vector $\langle x, y, z\rangle$ is

$\langle x, y, z\rangle^n = r^n\langle\sin(n\theta)\cos(n\phi),\sin(n\theta)\sin(n\phi),\cos(n\theta)\rangle$

where

$\begin{align}r&=\sqrt{x^2+y^2+z^2} \\ \phi&=\arctan(y/x)=\arg (x+yi) \\ {\rm and\ } \theta&=\arctan(\sqrt{x^2+y^2}/z)=\arccos(z/r).\end{align}$

They use the iteration $z\mapsto z^n+c$ where z^n is defined as above and a+b is a vector addition.^[2] For n > 3, the result is a 3-dimensional bulb-like structure with fractal surface detail and a number of "lobes" controlled by the parameter n. Many of their graphic renderings use n = 8.

Quadratic formula

Other forumulae come from identities which parametrise the sum of squares to give a power of the sum of squares such as:

(x² − y² − z²)² + (2xz)² + (2xy)² = (x² + y² + z²)²

which we can think of as a way to square a triplet of numbers so that the modulus is squared. So this gives, for example:

$x\rightarrow x^2-y^2-z^2+x_0$

$y\rightarrow 2 x z+y_0$

$z\rightarrow 2 x y +z_0$

or various other permutations. This 'quadratic' formula can be applied several times to get many power-2 formula.

Cubic formula

Cubic fractal

Other forumulae come from identities which parametrise the sum of squares to give a power of the sum of squares such as:

(x³ − 3xy² − 3xz²)² + (y³ − 3yx² + yz²)² + (z³ − 3zx² + zy²)² = (x² + y² + z²)³

which we can think of as a way to cube a triplet of numbers so that the modulus is cubed. So this gives:

$x\rightarrow x^3 - 3 x (y^2 + z^2) + x_0$

or other permutations.

$y\rightarrow -y^3 + 3 y x^2 - y z^2 + y_0$

$z\rightarrow z^3 - 3 z x^2 + z y^2 + z_0$

for example. Which reduces to the complex fractal $w\rightarrow w^3+w_0$ when z=0 and $w\rightarrow \overline{w}^3+w_0$ when y=0.

There are several ways to combine two such `cubic` transforms to get a power-9 transform which has slightly more structure.

Quintic formula

Quintic Mandelbulb

Quintic Mandelbulb with C=2

Another way to create Mandelbulbs with cubic symmetry is by taking the complex iteration formula $z\rightarrow z^{4m+1} + z_0$ for some integer m and adding terms to make it symmetrical in 3 dimensions but keeping the cross-sections to be the same 2 dimensional fractal. (The 4 comes from the fact that i⁴ = 1.) For example, take the case of $z\rightarrow z^5 + z_0$. In two dimensions where z = x + iy this is:

$x\rightarrow x^5-10 x^3 y^2 + 5 x y^4 + x_0$

$y\rightarrow y^5-10 y^3 x^2 + 5 y x^4 + y_0$

This can be then extended to three dimensions to give:

$x\rightarrow x^5 - 10 x^3 (y^2 + A y z + z^2) + 5 x (y^4 + B y^3 z + C y^2 z^2 + B y z^3 + z^4) + D x^2 y z (y+z) + x_0$

$y\rightarrow y^5 - 10 y^3 (z^2 + A x z + x^2) + 5 y (z^4 + B z^3 x + C z^2 x^2 + B z x^3 + x^4) + D y^2 z x (z+x)+ y_0$

$z\rightarrow z^5 - 10 z^3 (x^2 + A x y + y^2) + 5 z (x^4 + B x^3 y + C x^2 y^2 + B x y^3 + y^4) + D z^2 x y (x+y) +z_0$

for arbitrary constants A,B,C and D which give different Mandelbulbs (usually set to 0). The case $z \rightarrow z^9$ gives a Mandelbulb most similar to the first example where n=9. An more pleasing result for the fifth power is got basing it on the formula: $z\rightarrow -z^5 + z_0$.

Fractal based on z->-z^5

Power Nine formula

Fractal with z^9 Mandelbrot cross sections

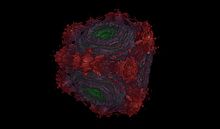
This fractal has cross-sections of the power 9 Mandelbrot fractal. It has 32 small bulbs sprouting from the main sphere. It is defined by, for example:

$x\rightarrow x^9-36 x^7 (y^2+z^2)+126 x^5 (y^2+z^2)^2-84 x^3 (y^2+z^2)^3+9 x (y^2+z^2)^4 + x_0$

$y\rightarrow y^9-36 y^7 (z^2+x^2)+126 y^5 (z^2+x^2)^2-84 y^3 (z^2+x^2)^3+9 y (z^2+x^2)^4 + y_0$

$z\rightarrow z^9-36 z^7 (x^2+y^2)+126 z^5 (x^2+y^2)^2-84 z^3 (x^2+y^2)^3+9 z (x^2+y^2)^4 + z_0$

These formula can be written in a shorter way:

$x\rightarrow \frac{1}{2}(x+i\sqrt{y^2+z^2})^9+\frac{1}{2}(x-i\sqrt{y^2+z^2})^9+x_0$

and equivalently for the other coordinates.

Power nine fractal detail

Spherical Formula

A perfect spherical formula can be defined as a formula:

$(x,y,z)\rightarrow( f(x,y,z)+x_0, g(x,y,z) + y_0, h(x,y,z) + z_0 )$

where

(x² + y² + z²)ⁿ = f(x,y,z)² + g(x,y,z)² + h(x,y,z)²

where f,g and h are nth power rational trinomials and n is an integer. The cubic fractal above is an example.

Taffy

Shapes with long strands are commonly described as looking like taffy and are considered less appealing.

Idealised 3D Mandelbrot Fractal

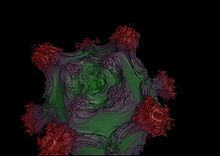
In the fractal community an idealised 3D Mandelbrot is considered to resemble a hierarchy of spheres just as the 2D Mandelbrot resembles a hierarchy of circles. The branch like structures of the 2D Mandelbrot should become twig-like structures of the 3D Mandelbrot. Such a fractal is considered the 'Holy Grail' of 3D fractal art.

See also

• Mandelbox
• List of fractals by Hausdorff dimension

References

1. ^ "Hypercomplex fractals". http://www.bugman123.com/Hypercomplex/index.html. 
2. ^ "Mandelbulb: The Unravelling of the Real 3D Mandelbrot Fractal". http://www.skytopia.com/project/fractal/2mandelbulb.html.  see "formula" section

External links

• Mandelbulb: The Unravelling of the Real 3D Mandelbrot Fractal, on Daniel White's website
• Several variants of the Mandelbulb, on Paul Nylander's website
• An opensource fractal renderer that can be used to create images of the Mandelbulb
• Mandelbulb/Juliabulb/Juliusbulb with examples of real 3D objects