Doubochinski's pendulum

Fig.1. Schematics of the Doubochinski’s pendulum

Doubochinski’s pendulum is a classical oscillator interacting with a high-frequency field in such a way that the oscillator takes on a discrete set of stable regimes of oscillation, each at a frequency near to the proper frequency of the oscillator, but each with a distinct, "quantized" amplitude. The phenomenon of amplitude quantization in this sort of coupled system was first discovered by the brothers Danil and Yakov Doubochinski in 1968–69.

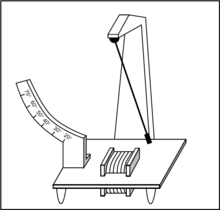
A simple demonstration apparatus consists of a mechanical pendulum interacting with a magnetic field (Fig. 1). The system is composed of two interacting oscillatory processes: (1) a pendulum arm with a natural frequency on the order of 0.5–1 Hz, with a small permanent magnet fixed at its moving end; and (2) a stationary electromagnet (solenoid) positioned under the equilibrium point of the pendulum’s trajectory and supplied with alternating current of fixed frequency, typically in the range of 10–1000 Hz. The mechanical pendulum arm and solenoid are configured in such a way, that the pendulum arm interacts with the oscillating magnetic field of the solenoid only over a limited portion of its trajectory – the so-called "zone of interaction" – outside of which the strength of the magnetic field drops off rapidly to zero. This spatial inhomogeniety of the interaction is key to the quantized behavior and other unusual properties of the system.

Fig.2. First four quantized amplitudes of Doubochinski’s pendulum at a magnetic field frequency f=50Hz. Solenoid is located at the bottom of the pendulum.

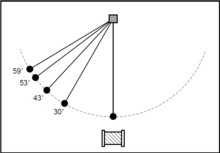
When released at any arbitrary starting position, the pendulum’s motion evolves into one of a discrete set of stable oscillation modes, having sharply differing amplitudes, but approximately the same period of oscillation – close to the pendulum’s undisturbed period (Fig. 2). In each such mode, the energy lost by friction in the pendulum’s motion, is compensated by an average net energy transfer from the oscillating magnetic field, in a self-regulating manner. The stability of each amplitude-mode is maintained by a constant self-adjustment of the phase relationship between the pendulum and the high-frequency field. Through its interaction with the field, the pendulum extracts the amount of energy needed to compensate its frictional losses for a given period. The pendulum compensates for the changes in the strength of the magnetic field, by slightly shifting the phase of its entry into the zone of interaction, while maintaining almost exactly the same amplitude and frequency. The values of the quantized amplitudes – and the corresponding energies of the quantized modes – are essentially independent of the strength of the alternating current supplied to the electromagnet, over a very large range. The higher the applied frequency, the larger the array of stable modes that become accessible to the pendulum (See Table 1).

Table 1. The stable quantized amplitudes of the Doubochinski pendulum

Frequency of the magnetic field (Hz)	Pendulum amplitudes
5					68°
20	30°			59°		74°		85°
30	30°	43°	53°	59°	68°	74°	80°	85°

References

• D.B. Doubochinski; Ya.B. Doubochinski (1991). "Amorçage argumen-taire d’oscillations entretenues avec une série discrète d’amplitudes stable". EDF Bulletin de la direction des études et recherches, série C, Mathématiques, Informatique: 11–20. 

• J. Tennenbaum (Winter 2005). "Amplitude Quantization as an Elementary Property of Macroscopic. Vibrating Systems". 21st Century Science & Technology. http://www.21stcenturysciencetech.com/2006_articles/Amplitude.W05.pdf. 

• L.A. Vainshtein; Ya.B. Doubochinski (1978). Zh. Tekh. Fiz [Sov. Phys.-Tech. Phys]. 48 [23]: 1321 [745]. 

• D.B. Doubochinski; Ya.B. Doubochinski (1982). "Wave excitation of an oscillator having a discrete series of stable amplitudes". Dokl. Akad. Nauk SSSR [Sov. Phys. Doklady]. 3 [27]: 605 [564]. 

• P.S. Landa (2001). Nonlinear Oscillations and Waves in Dynamical Systems. Department of Physics, Moscow State University, Moscow, Russia: Kluwer Academic Publishers. pp. 307. http://www.gbv.de/dms/goettingen/193719193.pdf. 

• V.N. Damgov; D.B. Duboshinskii; Ia.B. Duboshinskii (1986). The excitation of undamped oscillations with a discrete series of stable amplitudes. SAO/NASA ADS. Bibcode 1986BlDok..39...47D. 

• V. Damgov; I. Popov (1989). "Discrete" Oscillations and Multiple Attractors in Kick-excited Systems. pp. 2, 3, 25, 26. http://downloads.hindawi.com/journals/ddns/2000/985784.pdf. 

• P.S Landa; Y.B. Duboshinskii (1989). Self-oscillatory systems with high-frequency energy sources. Turpion Limited. http://www.turpion.org/php/reference.phtml?journal_id=pu&paper_id=2750&volume=32&issue=8&type=xrf. 

• D.I.Penner; D.B.Duboshinskiĭ (1973). "Asynchronous excitation of undamped oscillations". Soviet Physics Uspekhi 16 (1): 158–160. doi:10.1070/PU1973v016n01ABEH005156. http://iopscience.iop.org/0038-5670/16/1/A13;jsessionid=0F6175955F28F2EE19CCAA36B1F61DB0.c3. 

• D.B. Doubochinski; Ya.B. Duboshinsky et al (1979). "Discrete modes of a system subject to an inhomogeneous high-frequency force". Zh. Tech. Fiz [Sov. Phys.-Tech. Phys]. 49 [24]: 1160 [642]. 

• D. Doubochinski; J. Tennenbaum (2007). "The Macroscopic Quantum Effect in Nonlinear Oscillating Systems: a Possible Bridge between Classical and Quantum Physics". Cornell University Library "ARXIV". arXiv:0711.4892. 

• D. Doubochinski; J. Tennenbaum (2008). "On the Fundamental Properties of Coupled Oscillating Systems". Cornell University Library "ARXIV". arXiv:0712.2575. 

• D. Doubochinski; J. Tennenbaum (2008). "On the General Nature of Physical Objects and their Interactions, as Suggested by the Properties of Argumentally-Coupled Oscillating Systems". Cornell University Library "ARXIV". arXiv:0808.1205. 

• "Doubochinski’s site". http://www.doubochinski.com.