Trammel of Archimedes

Trammel of Archimedes.

A trammel of Archimedes is a mechanism that traces out an ellipse.^[1] It consists of two shuttles which are confined ('trammelled') to perpendicular channels or rails, and a rod which is attached to the shuttles by pivots at fixed positions along the rod. As the shuttles move back and forth, each along its channel, the end of the rod moves in an elliptical path. The semi-axes a and b of the ellipse are the distances between the end of the rod and the two pivots. An ellipsograph is a trammel of Archimedes intended to draw, cut, or machine ellipses, e.g. in wood or other sheet materials. An ellipsograph has the appropriate instrument (pencil, knife, router, etc.) attached to the rod. Usually the distances a and b are adjustable, so that the size and shape of the ellipse can be varied.

The history of such ellipsographs is not certain but they are believed to date back to Proclus and perhaps even to the time of Archimedes.^[2]

An animation of a Trammel of Archimedes in action.

Wooden versions of the trammel of Archimedes have been produced also as toys or novelty items, and sold under the name of nothing grinders or do nothing machines. In these toys the drafting instrument is replaced by a crank handle, and the position of the sliding shuttles is usually fixed.

Mathematics

Diagram

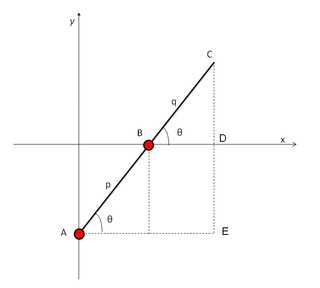
Let C be the end of the rod, and A, B be the pivots of the sliders. Let p and q be the distances from A to B and B to C, respectively. Let us assume that sliders A and B move along the y and x coordinate axes, respectively. When the rod makes an angle θ with the x-axis, the coordinates of point C are given by

$x = (p+q) \cos\theta\,$

$y = q \sin\theta\,$

These are the in the form of the standard parametric equations for an ellipse in canonical position.

Oblique trammel

The trammel of Archimedes is a special case of the more general oblique trammel. The axes constraining the pivots do not have to be perpendicular and the points A, B and C can form a triangle. The resulting locus of C is still an ellipse.^[2]

See also

• Beam compass

Notes

1. ^ Schwartzman, Steven (1996). The Words of Mathematics. The Mathematical Association of America. ISBN 0883855119.  (restricted online copy at Google Books)
2. ^ ^{a b} Wetzel, John E. (February 2010). "An Ancient Elliptic Locus". American Mathematical Monthly 117 (2): 161–167. JSTOR 10. 

References

• J. W. Downs: Practical Conic Sections: The Geometric Properties of Ellipses, Parabolas and Hyperbolas. Courier Dover 2003, ISBN 9780486428765, p. 4-5 (restricted online copy at Google Books)

External links

• Cutting ellipses in wood
• Photo of a Kentucky Do-Nothing
• Instructions on how to build a Kentucky Do-Nothing
• Video of a Do-Nothing made from Lego bricks
• "Wonky Trammel of Archimedes" An exploration of a generalized trammel.
• Patent for ellipse cutting guide allowing small ellipses