N-curve

We take the functional theoretic algebra C[0, 1] of curves. For each loop γ at 1, and each positive integer n, we define a curve γ_n called n-curve. The n-curves are interesting in two ways.

1. Their f-products, sums and differences give rise to many beautiful curves.
2. Using the n-curves, we can define a transformation of curves, called n-curving.

Multiplicative inverse of a curve

A curve γ in the functional theoretic algebra C[0, 1], is invertible, i.e.

$\gamma^{-1} \,$

exists if

$\gamma(0)\gamma(1) \neq 0. \,$

If γ ^* = (γ(0) + γ(1))e − γ, where $e(t)=1, \forall t \in [0, 1]$, then

$\gamma^{-1}= \frac{\gamma^{*}}{\gamma(0)\gamma(1)}.$

The set G of invertible curves is a non-commutative group under multiplication. Also the set H of loops at 1 is an Abelian subgroup of G. If $\gamma \in H$, then the mapping $\alpha \to \gamma^{-1}\cdot \alpha\cdot\gamma$ is an inner automorphism of the group G.

We use these concepts to define n-curves and n-curving.

n-Curves and their products

If x is a real number and [x] denotes the greatest integer not greater than x, then $x-[x] \in [0, 1].$

If $\gamma \in H$ and n is a positive integer, then define a curve γ_n by

$\gamma_n (t)=\gamma(nt - [nt]). \,$

γ_n is also a loop at 1 and we call it an n-curve. Note that every curve in H is a 1-curve.

Suppose $\alpha, \beta \in H.$ Then, since $\alpha(0)=\beta(1)=1, \mbox{ the f-product } \alpha \cdot \beta = \beta + \alpha -e$.

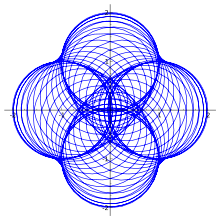
Example 1: Product of the astroid with the n-curve of the unit circle

Let us take u, the unit circle centered at the origin and α, the astroid. The n-curve of “u” is given by,

$u_n(t) = \cos(2\pi nt)+ i \sin(2\pi nt) \,$

and the astroid is

$\alpha(t)=\cos^{3}(2\pi t)+ i \sin^{3}(2\pi t), 0\leq t \leq 1$

The parametric equations of their product $\alpha \cdot u_{n}$ are

x = cos ³(2πt) + cos(2πnt) − 1,

y = sin ³(2πt) + sin(2πnt)

See the figure.

Since both α and u_n are loops at 1, so is the product.

N-curve with N = 53.

Animation of N-curve for N values from 0 to 50.

Example 2: Product of the unit circle and its n-curve

The unit circle is

$u(t) = \cos(2\pi t)+ i \sin(2\pi t) \,$

and its n-curve is

$u_n(t) = \cos(2\pi nt)+ i \sin(2\pi nt) \,$

The parametric equations of their product

$u \cdot u_{n}$

are

x = cos(2πnt) + cos(2πt) − 1,

y = sin(2πnt) + sin(2πt)

See the figure.

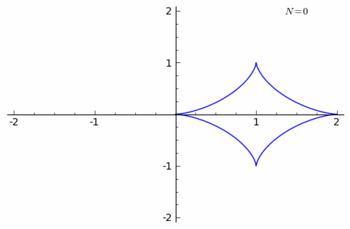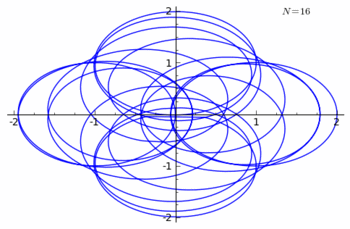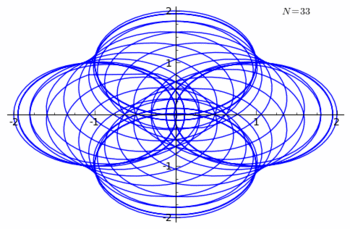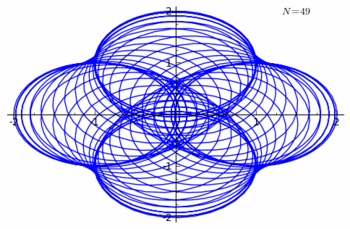
Example 3: n-Curve of the Rhodonea minus the Rhodonea curve

Let us take the Rhodonea Curve

r = cos(3θ)

If ρ denotes the curve,

$\rho(t) = \cos(6\pi t)[\cos(2\pi t) + i\sin(2\pi t)], 0 \leq t \leq 1$

The parametric equations of ρ_n − ρ are

x = cos(6πnt)cos(2πnt) − cos(6πt)cos(2πt),

$y = \cos(6\pi nt)\sin(2\pi nt)-\cos(6\pi t)\sin(2\pi t), 0 \leq t \leq 1$

n-Curving

If $\gamma \in H$, then, as mentioned above, the n-curve $\gamma_{n} \mbox{ also } \in H$. Therefore the mapping $\alpha \to \gamma_n^{-1}\cdot \alpha\cdot\gamma_n$ is an inner automorphism of the group G. We extend this map to the whole of C[0, 1], denote it by $\phi_{\gamma_n,e}$ and call it n-curving with γ. It can be verified that

$\phi_{\gamma_n ,e}(\alpha)=\alpha + [\alpha(1)-\alpha(0)](\gamma_{n}-1)e. \$

This new curve has the same initial and end points as α.

Example 1 of n-curving

Let ρ denote the Rhodonea curve r = cos(2θ), which is a loop at 1. Its parametric equations are

x = cos(4πt)cos(2πt),

$y = \cos(4\pi t)\sin(2\pi t), 0\leq t \leq 1$

With the loop ρ we shall n-curve the cosine curve

$c(t)=2\pi t + i \cos(2\pi t),\quad 0 \leq t \leq 1. \,$

The curve $\phi_{\rho_{n},e}(c)$ has the parametric equations

$x=2\pi[t-1+\cos(4\pi nt)\cos(2\pi nt)], \quad y=\cos(2\pi t)+ 2\pi \cos(4\pi nt)\sin(2\pi nt)$

See the figure.

It is a curve that starts at the point (0, 1) and ends at (2π, 1).

Notice how the curve starts with a cosine curve at N=0. Please note that the parametric equation was modified to center the curve at origin.

Example 2 of n-curving

Let χ denote the Cosine Curve

$\chi(t) = 2\pi t +i\cos(2\pi t), 0\leq t \leq 1$

With another Rhodonea Curve

ρ = cos(3θ)

we shall n-curve the cosine curve.

The rhodonea curve can also be given as

$\rho(t) = \cos(6\pi t)[\cos (2\pi t)+ i\sin(2\pi t)], 0\leq t \leq 1$

The curve $\phi_{\rho_{n},e}(\chi)$ has the parametric equations

x = 2πt + 2π[cos(6πnt)cos(2πnt) − 1],

$y=\cos(2\pi t) + 2\pi \cos( 6\pi nt)\sin(2 \pi nt), 0\leq t \leq 1$

See the figure for n = 15.

Generalized n-Curving

In the FTA C[0, 1] of curves, instead of e we shall take an arbitrary curve β, a loop at 1. This is justified since

L₁(β) = L₂(β) = 1

Then, for a curve γ in C[0, 1],

γ ^* = (γ(0) + γ(1))β − γ

and

$\gamma^{-1}= \frac{\gamma^{*}}{\gamma(0)\gamma(1)}.$

If $\alpha \in H$, the mapping

$\phi_{\alpha_n,\beta}$

given by

$\phi_{\alpha_n,\beta}(\gamma) = \alpha_n^{-1}\cdot \gamma \cdot \alpha_n$

is the n-curving. 

We get the formula

$\phi_{\alpha_n ,\beta}(\gamma)=\gamma + [\gamma(1)-\gamma(0)](\alpha_{n}-\beta).$

Thus given any two loops α and β at 1, we get a transformation of curve

γ given by the above formula.

This we shall call generalized n-curving.

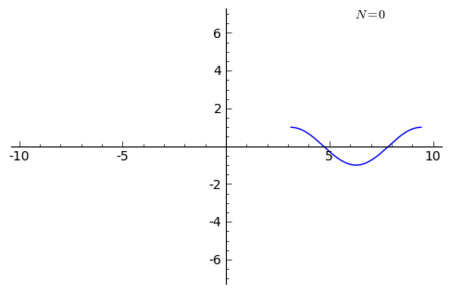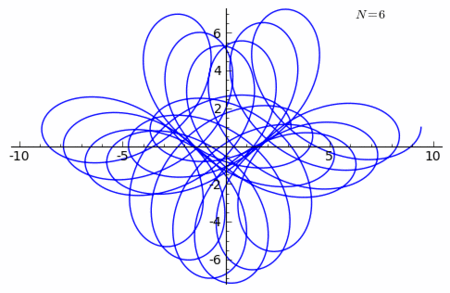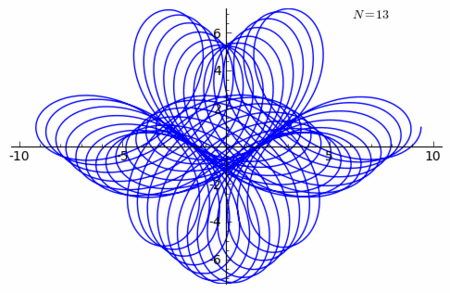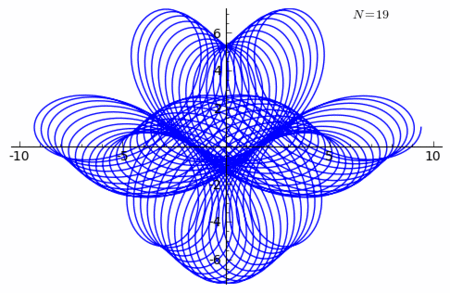
Example 1

Let us take α and β as the unit circle ``u.’’ and γ as the cosine curve

$\gamma (t) = 4\pi t + i\cos(4\pi t) 0 \leq t \leq 1$

Note that γ(1) − γ(0) = 4π

For the transformed curve for n = 40, see the figure.

The transformed curve $\phi_{u_n, u}( \gamma )$ has the parametric equations

Example 2

Denote the curve called Crooked Egg by η whose polar equation is

r = cos ³θ + sin ³θ

Its parametric equations are

x = cos(2πt)(cos ³2πt + sin ³2πt),

y = sin(2πt)(cos ³2πt + sin ³2πt)

Let us take α = η and β = u,

where u is the unit circle.

The n-curved Archimedean spiral has the parametric equations

x = 2πtcos(2πt) + 2π[(cos ³2πnt + sin ³2πnt)cos(2πnt) − cos(2πt)],

y = 2πtsin(2πt) + 2π[(cos ³2πnt) + sin ³2πnt)sin(2πnt) − sin(2πt)]

See the figures, the Crooked Egg and the transformed Spiral for n = 20.

See also

• Functional-theoretic algebra

References

• Sebastian Vattamattam, "Transforming Curves by n-Curving", in Bulletin of Kerala Mathematics Association, Vol. 5, No. 1, December 2008