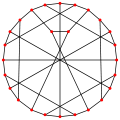
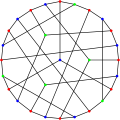
Coxeter graph

This article is about the 3-regular graph. For the graph associated with a Coxeter group, see Coxeter diagram.

Coxeter graph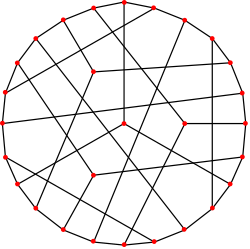
The Coxeter graph
Vertices	28
Edges	42
Radius	4
Diameter	4
Girth	7
Automorphisms	336 (PGL2(7))
Chromatic number	3
Chromatic index	3
Properties	Symmetric Distance-regular Distance-transitive Cubic Hypohamiltonian
v · mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges.[1] All the cubic distance-regular graphs are known.[2] The Coxeter graph is one of the 13 such graphs. It has chromatic number 3, chromatic index 3, radius 4, diameter 4 and girth 7. It is also a 3-vertex-connected graph and a 3-edge-connected graph. The Coxeter graph is hypohamiltonian : it does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from it is Hamiltonian. It has rectilinear crossing number 11, and is the smallest cubic graph with that crossing number currently known, but an 11-crossing, 26-vertex graph may exist (sequence A110507 in OEIS). Algebraic properties The automorphism group of the Coxeter graph is a group of order 336.[3] It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Coxeter graph is a symmetric graph. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Coxeter graph, referenced as F28A, is the only cubic symmetric graph on 28 vertices.[4] The Coxeter graph is also uniquely determined by the its graph spectrum, the set of graph eigenvalues of its adjacency matrix.[5] As a finite connected vertex-transitive graph that contains no Hamiltonian cycle, the Coxeter graph is a counterexample to a variant of the Lovász conjecture, but the canonical formulation of the conjecture asks for an Hamiltonian path and is verified by the Coxeter graph. Only five examples of vertex-transitive graph with no Hamiltonian cycles are known : the complete graph K2, the Petersen graph, the Coxeter graph and two graphs derived from the Petersen and Coxeter graphs by replacing each vertex with a triangle.[6] The characteristic polynomial of the Coxeter graph is (x − 3)(x − 2)8(x + 1)7(x2 + 2x − 1)6. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum. Gallery The graph obtained by any edge excision from the Coxeter is Hamilton-connected. The chromatic number of the Coxeter graph is 3. The rectilinear crossing number of the Coxeter graph is 11. References ^ Weisstein, Eric W., "Coxeter Graph" from MathWorld. ^ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance-Regular Graphs. New York: Springer-Verlag, 1989. ^ Royle, G. F028A data ^ Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002. ^ E. R. van Dam and W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Algebraic Combin. 15, pages 189-202, 2003 ^ Royle, G. "Cubic Symmetric Graphs (The Foster Census)." Wikimedia Foundation. 2010. Игры ⚽ Нужна курсовая? Tilting theory Coxeter notation Look at other dictionaries: Tutte–Coxeter graph — infobox graph name = Tutte–Coxeter graph image caption = namesake = W. T. Tutte H. S. M. Coxeter vertices = 30 edges = 45 girth = 8 chromatic number = 2 chromatic index = properties = Cubic Cage Moore graph Arc transitiveIn the mathematical field …   Wikipedia Coxeter group — In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry …   Wikipedia Coxeter–Dynkin diagram — See also: Dynkin diagram Coxeter Dynkin diagrams for the fundamental finite Coxeter groups …   Wikipedia Coxeter-Dynkin diagram — In geometry, a Coxeter Dynkin diagram is a graph with labelled edges. It represents the spatial relations between a collection of mirrors (or reflecting hyperplanes), and describes a kaleidoscopic construction.The diagram represents a Coxeter… …   Wikipedia Graphe de Coxeter — Représentation du graphe de Coxeter. Nombre de sommets 28 Nombre d arêtes 42 Distribution des degrés 3 régulier Rayon 4 …   Wikipédia en Français Graphe De Coxeter — Le graphe de Coxeter Nombre de sommets 28 Nombre d arêtes 42 Distribution des degrés 3 régulier Diamètre 4 Propriétés Hypohamilton …   Wikipédia en Français Graphe de coxeter — Le graphe de Coxeter Nombre de sommets 28 Nombre d arêtes 42 Distribution des degrés 3 régulier Diamètre 4 Propriétés Hypohamilton …   Wikipédia en Français Cubic graph — Not to be confused with graphs of cubic functions. The Petersen graph is a Cubic graph …   Wikipedia Crossing number (graph theory) — A drawing of the Heawood graph with three crossings. This is the minimum number of crossings among all drawings of this graph, so the graph has crossing number cr(G) = 3. In graph theory, the crossing number cr(G) of a graph G is the… …   Wikipedia Distance-transitive graph — The Biggs Smith graph, the largest 3 regular distance transitive graph. Graph families defined by their automorphisms distance transitive …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”