Comparison of the Hare and Droop quotas

In elections that use the single transferable vote (STV) method, quotas are used (a) for the determination of candidates considered elected; and (b) for the calculation of surplus votes to be redistributed.^[1] Two quotas in common use are the Hare quota and the Droop quota.

General comparison

The earliest versions of STV used the Hare quota. The Hare quota is equal to the total valid poll (V) divided by the total number of seats (n), or V / n.

The Droop quota is smaller than the Hare quota, and was first suggested ^[2] because it is the smallest quota that, like the Hare quota, ensures that the number of candidates who reach the quota will not be greater than the number of seats to be filled. Any quota smaller than the Droop quota carries a real, or at least theoretical, risk of more candidates being elected than there are seats to be filled. The Droop quota is the next integer larger than V / (n+1).

The difference between the two quotas comes down to what the quota implies. Winners elected under a Hare system represent that proportion of the electorate; winners under a Droop system were elected by that proportion of the electorate.

In an STV election in which there is only one seat to be filled (in other words an Instant Run-off Voting election) it is possible to use the Hare quota, which will simply be equal to 100% of votes cast. However, it is more efficient to use the Droop quota, which will be equal to an absolute majority of votes cast, meaning 50% plus one, and both quotas will achieve the same result. When voters have only one vote—the single non-transferable vote system—a candidate is sure to win if reaching the Droop quota.

In an STV election in which there are multiple winners the situation is slightly different, particularly with respect to the final seat.

• The Hare quota is generally kinder to small parties than the Droop quota because they have a better chance to win the final seat. Elected winners with the Hare quota more closely represent the proportionality of the electorate, and this can mean more proportional results for small parties. But this comes at the expense of emphasising the principle of majority rule. In an open list election held under the Hare quota it is possible for a group of candidates supported by a majority of voters to receive only a minority of seats if those voters do not disperse their vote relatively evenly across all their supported candidates, see Scenario 1 below. In contrast, such an outcome will not happen in an election held under the Droop quota unless voters in the majority do not rank all their preferred candidates or not enough preferred candidates seek office.
• The Droop quota is generally kinder to large parties because they have a better chance to win the final seat. This comes at the expense of emphasising the principle of proportional representation. In an election held under the Droop quota it is possible for a group of candidates to over-represent a proportion of voters even though a majority of the remaining voters support a minor party, see Scenario 2 below.

The Droop quota is today the most popular quota for STV elections - and almost universal for government STV elections - for two reasons^{[citation needed]}. First, because it can more efficiently elect candidates in the each round of distribution of seats (whether STV or list PR) than is the case with the Hare quota. Second, because the possibility under the Hare quota that a group of candidates supported by a majority of voters to receive only a minority of seats is considered undemocratic^{[citation needed]}.

Examples of the different outcomes between the Hare and the Droop quotas follow:

Scenario 1

An example with an open list where the result under the Droop quota more closely reflects the support that voters have for a party, irrespective of the support they have for individuals within the party.

Imagine an election in which there are 5 seats to be filled. There are 6 candidates divided between two groups: Andrea, Carter and Brad are members of the Alpha party; Delilah, Scott and Jennifer are members of the Beta party. There are 120 voters and they vote as follows:

Alpha party			Beta party
31 voters Andrea Carter Brad	30 voters Carter Andrea Brad	2 voters Brad Andrea Carter	20 voters Delilah Scott Jennifer	20 voters Scott Delilah Jennifer	17 voters Jennifer Delilah Scott

It can be seen that supporters of the Alpha party all rank all three Alpha party candidates higher than any of the Beta party candidates (the final three preferences of the voters are not shown above because they will not affect the result of the election). Similarly, voters who support the Beta party all give their first three preferences to Beta party candidates. Overall, the Alpha party receives 63 votes out of a total of 120 votes. The Alpha party therefore has a majority of about 53%. The Beta party receives a 47% share of the vote.

Below the election results are shown first under the Hare quota and then under the Droop quota. It can be seen that under the Hare quota, despite receiving 53% of the vote, the Alpha party receives only a minority of seats. When the same election is conducted under the Droop quota, however, the Alpha party's majority is rewarded with a majority of seats.

Note that this issue can be avoided under the Hare quota if the Robson Rotation is used to randomly order the party candidates.

Count under the Hare quota The Hare quota is calculated as 24. When first preferences are tallied Andrea and Carter have both reached a quota and are declared elected. Andrea has a surplus of 7 and Carter has a surplus of 6. Both surpluses are transferred to Brad (who is of the same party) so the tallies become: Brad (Alpha party): 15 Delilah (Beta party): 20 Scott (Beta party): 20 Jennifer (Beta party): 17 No candidate has reached a quota. Brad is the candidate with the fewest votes and so he is excluded. Because just three candidates remain and there are only three more seats to be filled, Delilah, Scott and Jennifer are all declared elected. Result: The elected candidates are: Andrea and Carter (from the Alpha party), and Delilah, Scott and Jennifer (from the Beta party).

Count under the Droop quota The Droop quota is calculated as 20. When first preferences are tallied Andrea and Carter have reached the quota and, as before, are declared elected. However this time Andrea has a surplus of 11 and Carter a surplus of 10. These surpluses transfer to Brad and the tallies become: Brad (Alpha party): 23 Delilah (Beta party): 20 Scott (Beta party): 20 Jennifer (Beta party): 17 Brad has now reached a quota and is declared elected. He has no surplus so Jennifer, who this time has the fewest votes, is excluded. Because only Delilah and Scott are left in the count, and there are only two seats left to fill, they are both declared elected. Result: The elected candidates are Andrea, Carter and Brad (from the Alpha party) and Delilah and Scott (from the Beta party).

Scenario 2

An example with a closed list where the result under the Hare quota more closely reflects the proportion of voters that support each party than the result under the Droop quota.

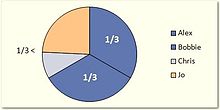
Imagine an election in which there are 3 seats to be filled. There are 4 candidates divided between two groups: Alex, Bobbie and Chris are members of the Alpha party; Jo is a member of the Beta party. There are 99 voters and they vote as follows:

Alpha party	Beta party
75 voters Alex Bobbie Chris	24 voters Jo

Count under the Hare quota The Hare quota is calculated as 33. When first preferences are tallied Alpha party has two full quotas so Alex and Bobbie are declared elected. Alpha party has a surplus of 9 so the tallies become: Alpha Party (Chris) : 9 Beta Party (Jo): 24 No candidate has reached a quota. Alpha is the party with the fewest votes and so Chris is excluded. Because just one candidate remains and there is only one more seat to be filled, Jo is declared elected. Result: The elected candidates are: Alex and Bobbie (from the Alpha party), and Jo (from the Beta party).

Count under the Droop quota The Droop quota is calculated as 25. When first preferences are tallied Alpha party has three full quotas so Alex, Bobbie and Chris are declared elected. Alpha party has a surplus of 0. With three candidates elected there are no more seats to fill. Result: The elected candidates are Alex, Bobbie and Chris (from the Alpha party). The Beta party is excluded from representation and hence 24% of the voters are in effect disenfranchised.

Notes

1. ^ Hill, I.D. (1987). "Algorithm 123 — Single Transferable Vote by Meek’s method".
2. ^ Henry Richmond Droop, "On methods of electing representatives" in the Journal of the Statistical Society of London Vol. 44 No. 2 (June 1881) pp.141-196 [Discussion, 197-202], reprinted in Voting matters Issue 24 (October 2007) pp.7–46.

See also

• List of democracy and elections-related topics