Chebfun

Chebfun

Developer(s)	The Chebfun team, University of Oxford
Stable release	v4.1 / September 2011
Written in	MATLAB
Type	Numerical software
License	BSD
Website	Chebfun home page

Chebfun is a freely available software system written in MATLAB for numerical computation with functions of a real variable. It is based on the idea of overloading MATLAB's commands for vectors and matrices to analogous commands for functions and operators. Thus, for example, whereas the SUM command in MATLAB adds up the elements of a vector, the SUM command in Chebfun evaluates a definite integral. Similarly the backslash command in MATLAB becomes a Chebfun command for solving differential equations^[1].

The mathematical basis of Chebfun is numerical algorithms involving piecewise polynomial interpolants and Chebyshev polynomials, and this is where the name "Cheb" comes from. The package aims to combine the feel of symbolic computing systems like Maple and Mathematica with the speed of floating-point numerics^[2][3].

The Chebfun project is based in the Mathematical Institute at the University of Oxford and was initiated in 2002 by Lloyd N. Trefethen and his student Zachary Battles^[4]. The most recent version, Version 4.0, was released in February 2011.

Features

• Approximation of functions
• Quadrature
• Rootfinding
• 1D global optimisation
• Ordinary differential equations
• Partial differential equations

Example usage

A user may begin by initialising the variable x, on the interval [0,10], say.

>> x = chebfun('x',[0,10]);

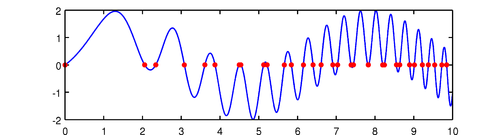
This variable can now be used to perform further computations, for example, computing and plotting roots of a function:

>> f = sin(x) + sin(x.^2);  plot(f)
>> r = roots(f); hold on, plot(r,f(r),'.r'), hold off

The definite integral can be computed with:

>> sum(f) 
ans 
   = 2.422742429006079

References

1. ^ Driscoll, Tobin A.; Bornemann, Folkmar; Trefethen, Lloyd N. (Nov. 22, 2008). "The Chebop system for automatic solution of differential equations". BIT Num. Math. 48: 701–723. http://www.springerlink.com/content/46471515240111m2/. 
2. ^ Trefethen, Lloyd N. (Oct. 23, 2007). "Computing numerically with functions instead of numbers". Birkhauser J. Math. Comput. Sci. 1: 9–19. http://www.springerlink.com/content/5083k3qu7t3g9042/. 
3. ^ Pachón, Ricardo; Platte, Rodrigo; Trefethen, Lloyd N. (2009). "Piecewise smooth Chebfuns". IMA J. Num. Analysis. http://imajna.oxfordjournals.org/content/early/2009/07/28/imanum.drp008.abstract. 
4. ^ Battles, Zachary3.1111; Trefethen, Lloyd N. (May 20, 2004). "An extension of MATLAB to continuous functions and operators". SIAM J. Sci. Comp. 25 (5): 1743–1770. http://siamdl.aip.org/vsearch/servlet/VerityServlet?KEY=SJOCE3&smode=strresults&sort=chron&maxdisp=25&threshold=0&pjournals=SJOCE3&possible1=battles&possible1zone=article&OUTLOG=NO&viewabs=SJOCE3&key=DISPLAY&docID=2&page=1&chapter=0. 

External links

• Homepage: Chebfun