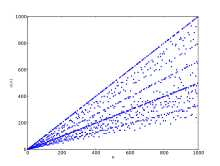
Euler's totient function

For other functions named after Euler, see List of topics named after Leonhard Euler.

The first thousand values of φ(n)

In number theory, the totient φ(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n (i.e. having no common positive factors other than 1). In particular φ(1) = 1 since 1 is coprime to itself (1 being the only natural number with this property). For example, φ(9) = 6 since the six numbers 1, 2, 4, 5, 7 and 8 are coprime to 9. The function φ so defined is the totient function. The totient is usually called the Euler totient or Euler's totient, after the Swiss mathematician Leonhard Euler, who studied it. The totient function is also called Euler's phi function or simply the phi function, since it is commonly denoted by the Greek letter phi (φ). The cototient of n is defined as n − φ(n), in other words the number of positive integers less than or equal to n that are not coprime to n.

The totient function is important mainly because it gives the size of the multiplicative group of integers modulo n. More precisely, φ(n) is the order of the group of units of the ring $\mathbb{Z}/n\mathbb{Z}$. This fact, together with Lagrange's theorem on the possible sizes of subgroups of a group, provides a proof for Euler's theorem that $a^{\varphi(n)}\equiv 1 \pmod{n}$ for all a coprime to n. The totient function also plays a key role in the definition of the RSA encryption system.

Computing Euler's function

The totient φ is a multiplicative function; if m and n are coprime then φ(mn) = φ(m)φ(n). (Sketch of proof: let A, B, C be the sets of residue classes modulo-and-coprime-to m, n, mn respectively; then there is a bijection between A × B and C, by the Chinese remainder theorem.)

If n = p^k, where p is prime, then $\varphi(n) = p^k -p^{k-1} = p^k \left( 1 - \frac{1}{p} \right)$.

Proof: It is easy to list all positive integers that are less than or equal to p^k and not relatively prime to p^k. They are $p, 2p, 3p, \cdots,p^{k-1}p = p^k$. They are all multiples of p and we have exactly p^{k − 1} of them. Therefore, there are exactly p^k − p^{k − 1} = (p − 1)p^{k − 1} positive integers less than or equal to p^k that are relatively prime to p^k.

The value of φ(n) for n > 1 can thus be computed using the fundamental theorem of arithmetic: if

$n = p_1^{k_1} \cdots p_r^{k_r}$

where each p_i is a distinct prime, then

$\varphi(n)=(p_1-1)p_1^{k_1-1} \times (p_2-1)p_2^{k_2-1} \cdots \times(p_r-1)p_r^{k_r-1}.$

This last formula is an Euler product and is often written in the equivalent form (multiplying top and bottom by $n=p_1^{k_1} \cdots p_r^{k_r}$)

$\varphi(n)= n(p_1-1)p_1^{-1} \times (p_2-1)p_2^{-1} \cdots \times(p_r-1)p_r^{-1}=n \cdot \prod_{p|n} \left( 1-\frac{1}{p} \right)$

with the product ranging only over the distinct primes p dividing n.

Proof: Repeatedly applying the above mentioned theorems that we get

$\varphi(n) = \varphi(p_1^{k_1}) \varphi(p_2^{k_2}) \cdots\varphi(p_r^{k_r})$

This can be rewritten as

$\varphi(n) = p_1^{k_1} \left(1- \frac{1}{p_1} \right) p_2^{k_2} \left(1- \frac{1}{p_2} \right) \cdots p_r^{k_r} \left(1- \frac{1}{p_r} \right)$

$= p_1^{k_1} p_2^{k_2} \cdots p_r^{k_r} \left(1- \frac{1}{p_1} \right) \left(1- \frac{1}{p_2} \right) \cdots \left(1- \frac{1}{p_r} \right)$

$=n \left(1- \frac{1}{p_1} \right)\left(1- \frac{1}{p_2} \right) \cdots\left(1- \frac{1}{p_r} \right)$

Computing example

$\varphi(36)=\varphi\left(2^2 3^2\right)=36\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)=36\cdot\frac{1}{2}\cdot\frac{2}{3}=12.$

In words, this says that the distinct prime factors of 36 are 2 and 3; half of the thirty-six integers from 1 to 36 are divisible by 2, leaving eighteen; a third of those are divisible by 3, leaving twelve coprime to 36. And indeed there are twelve: 1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, and 35.

Some values of the function

The first 99 values (sequence A000010 in OEIS) are shown in the table and graph below:

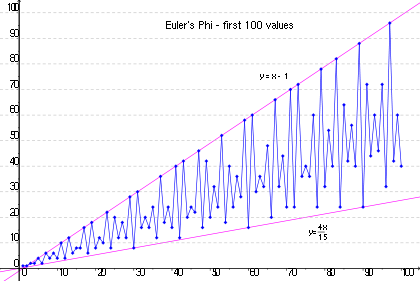Run chart of the first 100 values

φ(n)	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

Note that the lower bound of y = 4n/15 ≈ .267n only occurs where n is a multiple of 30. (This is not a lower bound for the whole totient function, but only for these first few values of n. For example, $\varphi(210) = 48 = 8(210)/35 \approx .22857 n$; $\varphi(2310) = 480 = 16(2310)/77 \approx .208 n$; and $\varphi(30030) = 5760 = 192(30030)/1001 \approx .192 n$.)

Properties

• φ(p^α) = p^α − p^{α − 1} for prime p and $\alpha \geq 1$.
• $\varphi(mn) = \varphi(m)\varphi(n)\cdot\frac{d}{\varphi(d)}$ where d = gcd(m,n).
• $\varphi(m) = \frac{1}{2}\varphi(2m)$ where m = 2k.
• φ(m) = φ(2m) where m = 2k+1.
• $\varphi(\mathrm{lcm}(m,n))\cdot\varphi(\mathrm{gcd}(m,n)) = \varphi(m)\cdot\varphi(n)$ (See lcm).
• $a\mid b$ implies $\varphi(a)\mid\varphi(b)$.
• φ(n) is even for $n \geq 3$. Moreover, if n has r distinct odd prime factors, $2^r \mid \varphi(n)$.
• Schramm (2008) has shown that:

  $\varphi (n)=\sum\limits_{k=1}^n{\operatorname{gcd}(k,n)\cdot \exp \left(\frac{-2\pi ik}{n}\right)}.$

The number φ(n) is also equal to the number of possible generators of the cyclic group C_n (and therefore also to the degree of the cyclotomic polynomial φ_n). Since every element of C_n generates a cyclic subgroup and the subgroups of C_n are of the form C_d where d divides n (written as d | n), we get

$\sum_{d\mid n}\varphi(d)=n$

where the sum extends over all positive divisors d of n.

We can now use the Möbius inversion formula to "invert" this sum and get another formula for φ(n):

$\varphi(n)=\sum_{d\mid n} d \cdot \mu\left(\frac{n}{d} \right)$

where μ is the usual Möbius function defined on the positive integers.

According to Euler's theorem, if a is coprime to n, that is, gcd(a, n) = 1, then

$a^{\varphi(n)} \equiv 1\mod n.\,$

This follows from Lagrange's theorem and the fact that a belongs to the multiplicative group of $\mathbb{Z}/n\mathbb{Z}$ iff a is coprime to n.

Generating functions

The two generating functions presented here are both consequences of the fact that

∑	φ(d) = n.
d | n

Which, in the notation of Dirichlet convolution of Multiplicative function, says:

φ * 1 = Id

The Dirichlet series for φ(n) may be written in terms of the Riemann zeta function by taking Dirichlet series of both sides and rearranging to get:

$\sum_{n=1}^\infty \frac{\varphi(n)}{n^s}=\frac{\zeta(s-1)}{\zeta(s)}$

A Lambert series generating function is

$\sum_{n=1}^{\infty} \frac{\varphi(n) q^n}{1-q^n}= \frac{q}{(1-q)^2}$

which converges for |q|<1.

This follows from

$\sum_{n=1}^{\infty} \frac{\varphi(n) q^n}{1-q^n} = \sum_{n=1}^{\infty} \varphi(n) \sum_{r=1}^{\infty} q^{rn}$

which is

$\sum_{k=1}^{\infty} q^k \sum_{n|k} \varphi(n) = \sum_{k=1}^{\infty} k q^k = \frac{q}{(1-q)^2}.$

Growth of the function

The growth of φ(n) as a function of n is an interesting question, since the first impression from small n that φ(n) might be noticeably smaller than n is somewhat misleading. Asymptotically we have

$\,n^{1-\varepsilon}<\varphi(n)<n$

for any given ε > 0 and n > N(ε). In fact if we consider

$\,\varphi(n)/n,$

we can write that, from the formula above, as the product of factors

$1-p^{-1}\,$

taken over the prime numbers p dividing n. Therefore the values of n corresponding to particularly small values of the ratio are those n that are the product of an initial segment of the sequence of all primes. From the prime number theorem it can be shown that a constant ε in the formula above can therefore be replaced by

$C\,\log \log n/ \log n.$

φ is also generally close to n in an average sense:

$\frac{1}{n^2} \sum_{k=1}^n \varphi(k)= \frac{3}{\pi^2} + \mathcal{O}\left(\frac{\log n }{n}\right)$

where the big O is the Landau symbol. This also says that the probability of two positive integers chosen at random from $\{1, 2, \ldots , n \}$ being relatively prime approaches $\frac{6}{\pi^2}$ when n tends to infinity. A related result is the average order of $\frac{\varphi(n)}{n}$, which is described by

$\frac{1}{n} \sum_{k=1}^n \frac{\varphi(k)}{k} = \frac{6}{\pi^2} + \mathcal{O}\left(\frac{\log n }{n}\right)$

Because $\frac{6}{\pi^2} = \frac{1}{\zeta(2)}$, one can also express the formula this way.

$\frac{1}{n} \sum_{k=1}^n \frac{\varphi(k)}{k} = \frac{1}{\zeta(2)} + \mathcal{O}\left(\frac{\log n }{n}\right)$

Other formulas involving Euler's function

• $\;\varphi\left(n^m\right) = n^{m-1}\varphi(n) \text{ for } m\ge 1$

• $\text{For any } a, n > 1 \text{, } n \mid \varphi(a^n-1)$

Because modulo aⁿ − 1, a has order n, but we also have $a^{\varphi(a^n - 1)} \equiv 1$

• For any a > 1 and n > 6 such that $4 \nmid n$ there exists an $l \geq 2n$ such that $l \mid \varphi(a^n-1)$.

• $\sum_{d \mid n} \frac{\mu^2(d)}{\varphi(d)} = \frac{n}{\varphi(n)}$

• $\sum_{1\le k\le n \atop (k,n)=1}\!\!k = \frac{1}{2}n\varphi(n)\text{ for }n>1$

• $\sum_{k=1}^n\varphi(k) = \frac{1}{2}\left(1+ \sum_{k=1}^n \mu(k)\left\lfloor\frac{n}{k}\right\rfloor^2\right)$

• $\sum_{k=1}^n\frac{\varphi(k)}{k} = \sum_{k=1}^n\frac{\mu(k)}{k}\left\lfloor\frac{n}{k}\right\rfloor$

• $\sum_{k=1}^n\frac{k}{\varphi(k)} = \mathcal{O}(n)$

• $\sum_{k=1}^n\frac{1}{\varphi(k)} = \mathcal{O}(\log(n))$

• $\sum_{1\le k\le n \atop (k,m)=1} 1 = n \frac {\varphi(m)}{m} + \mathcal{O} \left ( 2^{\omega(m)} \right ),$

where m > 1 is a positive integer and ω(m) designates the number of distinct prime factors of m. (This formula counts the number of naturals less than or equal to n and relatively prime to m, additional material is listed among the external links.)

Inequalities

Some inequalities involving the φ function are:

$\varphi(n) > \frac {n} {e^\gamma\; \log \log n + \frac {3} {\log \log n}}$ for n > 2, where γ is Euler's constant,^[1]

$\varphi(n) \ge \sqrt{\frac {n} {2} }$ for n > 0,

and

$\varphi(n) \ge \sqrt{n}\text{ for } n > 6.$

For prime n, clearly φ(n) = n − 1.

For a composite number n we have

$\varphi(n) \le n-\sqrt{n}$ .

For any even number 2n we have

$\varphi(2n) \le n$

where equality holds only if n is a power of two.

For arbitrarily large n, these bounds still cannot be improved, or to be more precise:

$\liminf \frac{\varphi (n)}{n}=0 \mbox{ and } \limsup \frac{\varphi (n)}{n}=1.$ The first bound follows by considering n as the product of the first k primes. The second follows from letting n range over the primes.^[2]

A pair of inequalities combining the φ function and the σ divisor function are:

$\frac {6 n^2}{\pi^2} < \varphi(n) \sigma(n) < n^2 \mbox{ for } n>1.$^[2]

Ford's theorem

Ford (1999) proved that for every integer k ≥ 2 there is a number m for which the equation φ(x) = m has exactly k solutions; this result had previously been conjectured by Wacław Sierpiński. However, no such m is known for k = 1, and according to Carmichael's totient function conjecture it is believed that in this case no such m exists.

See also

• Carmichael function
• Generalizations of Fermat's little theorem
• Multiplicative group of integers modulo n

Notes

1. ^ Bach, E.; Shallit, J. (1996), "Theorem 8.8.7", Algorithmic Number Theory, 1, Cambridge, MA: MIT Press, p. 234, ISBN 0-262-02405-5, http://books.google.com/books?id=iJx1lP9ZcIkC&pg=PA234 
2. ^ ^{a b} G.H. Hardy, E. M. Wright (1979), An Introduction to the Theory of Numbers (Fifth Edition), Oxford: Clarendon Press, pp. 267, ISBN 0 19 853171 0 

References

• Abramowitz, M.; Stegun, I. A. (1964), Handbook of Mathematical Functions, New York: Dover Publications, ISBN 0-486-61272-4 . See paragraph 24.3.2.

• Ford, K. (1999), "The number of solutions of φ(x) = m", Annals of Mathematics 150 (1): 283–311, doi:10.2307/121103, JSTOR 121103, MR1715326 .

• Schramm, Wolfgang (2008), "The Fourier transform of functions of the greatest common divisor", Electronic Journal of Combinatorial Number Theory A50 (8(1)), http://www.integers-ejcnt.org/vol8.html .

External links

• Kirby Urner, Computing totient function in Python and scheme, (2003)
• Euler's totient function calculator in JavaScript - up to 20 digits
• Miyata, Daisuke & Yamashita, Michinori, Derived logarithmic function of Euler's function
• Bordellès, Olivier, Numbers prime to q in [1,n]
• Plytage, Loomis, Polhill Summing Up The Euler Phi Function