Mandelstam variables

In this diagram, two particles come in with momenta p₁ and p₂, they interact in some fashion, and then two particles with different momentum (p₃ and p₄) leave.

In theoretical physics, the Mandelstam variables are numerical quantities that encode the energy, momentum, and angles of particles in a scattering process in a Lorentz-invariant fashion. They are used for scattering processes of two particles to two particles.

If the Minkowski Metric is chosen to be diag(1, − 1, − 1, − 1), the Mandelstam variables s,t,u are then defined by

• $s=(p_1+p_2)^2=(p_3+p_4)^2 \,$
• $t=(p_1-p_3)^2=(p_2-p_4)^2 \,$
• $u=(p_1-p_4)^2=(p_2-p_3)^2 \,$

Where p₁ and p₂ are the four-momenta of the incoming particles and p₃ and p₄ are the four-momenta of the outgoing particles, and we are using Planck units (c=1).

s is also known as the square of the center-of-mass energy (invariant mass) and t is also known as the square of the momentum transfer.

Feynman diagrams

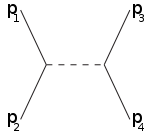
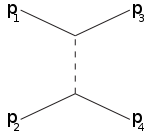
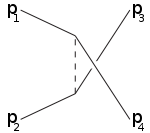
The letters s,t,u are also used in the terms s-channel, t-channel, u-channel. These channels represent different Feynman diagrams or different possible scattering events where the interaction involves the exchange of an intermediate particle whose squared four-momentum equals s,t,u, respectively.

s-channel	t-channel	u-channel

For example the s-channel corresponds to the particles 1,2 joining into an intermediate particle that eventually splits into 3,4: the s-channel is the only way that resonances and new unstable particles may be discovered provided their lifetimes are long enough that they are directly detectable. The t-channel represents the process in which the particle 1 emits the intermediate particle and becomes the final particle 3, while the particle 2 absorbs the intermediate particle and becomes 4. The u-channel is the t-channel with the role of the particles 3,4 interchanged.

The Mandelstam variables were first introduced by physicist Stanley Mandelstam in 1958.

Details

High-energy limit

In the relativistic limit rest mass can be neglected, so for example,

$s=(p_1+p_2)^2=p_1^2+p_2^2+2 p_1 \cdot p_2 \approx 2 p_1 \cdot p_2 \,$

because $p_1^2 = m_1^2$ and $p_2^2 = m_2^2.$ It is reminded that by relativistic limit one means that the momentum (speed) is so large that in the relativistic energy-momentum equation the energy becomes essentially the momentum norm (e.g. $E^2= \mathbf{p} \cdot \mathbf{p} + {m_0}^2 \text{ becomes } E^2 \approx \mathbf{p} \cdot \mathbf{p}$).

In summary,

$s \approx \,$	$2 p_1 \cdot p_2 \approx\,$	$2 p_3 \cdot p_4 \,$
$t \approx \,$	$-2 p_1 \cdot p_3 \approx \,$	$-2 p_2 \cdot p_4 \,$
$u \approx \,$	$-2 p_1 \cdot p_4 \approx \,$	$-2 p_3 \cdot p_2 \,$

Addition of

Note that

$s+t+u = m_1^2 + m_2^2 + m_3^2 + m_4^2 \,$

where m_i is the mass of particle i.

Proof

To prove this, we need to use two facts:

• The square of a particle's four momentum is the square of its mass,

$p_i^2 = m_i^2 \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (1) \,$

• And conservation of four-momentum,

$p_1 + p_2 = p_3 + p_4 \,$

$p_1 = -p_2 + p_3 + p_4 \quad \quad \quad \quad \quad \quad \quad (2)\,$

So, to begin,

$s=(p_1+p_2)^2=p_1^2 + p_2^2 + 2p_1 \cdot p_2 \,$

$t=(p_1-p_3)^2=p_1^2 + p_3^2 - 2p_1 \cdot p_3 \,$

$u=(p_1-p_4)^2=p_1^2 + p_4^2 - 2p_1 \cdot p_4 \,$

First, use (1) to re-write these,

$s=m_1^2 + m_2^2 + 2p_1 \cdot p_2 \,$

$t=m_1^2 + m_3^2 - 2p_1 \cdot p_3 \,$

$u=m_1^2 + m_4^2 - 2p_1 \cdot p_4 \,$

Then add them

$s+t+u \,$	$=3m_1^2 + m_2^2 + m_3^2 + m_4^2 + 2p_1 \cdot p_2 - 2p_1 \cdot p_3 - 2p_1 \cdot p_4 \,$
	$=m_1^2 + m_2^2 + m_3^2 + m_4^2 + 2 \left( m_1^2 + p_1 \cdot p_2 - p_1 \cdot p_3 - p_1 \cdot p_4 \right) \,$
	$=m_1^2 + m_2^2 + m_3^2 + m_4^2 + 2 \left( m_1^2 + p_1 \cdot \left( p_2 - p_3 - p_4 \right) \right) \,$

Then use eq (2) to simplify further,

$s+t+u \,$	$=m_1^2 + m_2^2 + m_3^2 + m_4^2 + 2 \left( m_1^2 - p_1 \cdot p_1 \right) \,$
	$=m_1^2 + m_2^2 + m_3^2 + m_4^2 + 2 \left( m_1^2 - m_1^2 \right) \,$

So finally,

$s+t+u = m_1^2 + m_2^2 + m_3^2 + m_4^2 \,$

See also

• Feynman diagrams
• Bhabha scattering
• Møller scattering
• Compton scattering

References

• Mandelstam, S. (1958). "Determination of the Pion-Nucleon Scattering Amplitude from Dispersion Relations and Unitarity". Physical Review 112 (4): 1344. Bibcode 1958PhRv..112.1344M. doi:10.1103/PhysRev.112.1344. http://dbserv.ihep.su/hist/owa/hw.part2?s_c=MANDELSTAM+1958. 
• Halzen, Francis; Martin, Alan (1984). Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons. ISBN 0-471-88741-2. 
• Perkins, Donald H. (2000). Introduction to High Energy Physics (4th ed.). Cambridge University Press. ISBN 0-521-62196-8.