Reassignment method

The method of reassignment is a technique forsharpening a time-frequency representation by mappingthe data to time-frequency coordinates that are nearer tothe true region of support of theanalyzed signal. The method has been independentlyintroduced by several parties under various names, including"method of reassignment", "remapping", "time-frequency reassignment", and "modified moving-window method". Inthe case of the spectrogram or the short-time Fourier transform, the method of reassignment sharpens blurrytime-frequency data by relocating the data according tolocal estimates of instantaneous frequency and group delay.This mapping to reassigned time-frequency coordinates isvery precise for signals that are separable in time andfrequency with respect to the analysis window.

Introduction

thumb|400px">
Reassigned spectral surface for the onset of an acoustic bass tone having a sharp pluck and a fundamental frequency of approximately 73.4 Hz.Sharp spectral ridges representing the harmonics are evident, as is theabrupt onset of the tone.The spectrogram was computed using a 65.7 ms Kaiser window with a shapingparameter of 12.

Many signals of interest have a distribution of energy thatvaries in time and frequency. For example, any sound signalhaving a beginning or an end has an energy distribution thatvaries in time, and most sounds exhibit considerablevariation in both time and frequency over their duration.Time-frequency representations are commonly used to analyzeor characterize such signals. They map the one-dimensionaltime-domain signal into a two-dimensional function of timeand frequency. A time-frequency representation describes thevariation of spectral energy distribution over time, much asa musical score describes the variation of musical pitchover time.

In audio signal analysis, the spectrogram is the mostcommonly-used time-frequency representation, probablybecause it is well-understood, and immune to so-called"cross-terms" that sometimes make other time-frequencyrepresentations difficult to interpret. But the windowingoperation required in spectrogram computation introduces anunsavory tradeoff between time resolution and frequencyresolution, so spectrograms provide a time-frequencyrepresentation that is blurred in time, in frequency, or inboth dimensions. The method of time-frequency reassignmentis a technique for refocussing time-frequency data in ablurred representation like the spectrogram by mapping thedata to time-frequency coordinates that are nearer to thetrue region of support of the analyzed signal.

The Spectrogram as a Time-Frequency Representation

One of the best-known time-frequency representations is thespectrogram, defined as the squared magnitude of theshort-time Fourier transform. Though the short-time phasespectrum is known to contain important temporal informationabout the signal, this information is difficult tointerpret, so typically, only the short-time magnitudespectrum is considered in short-time spectral analysis.

As a time-frequency representation, the spectrogram hasrelatively poor resolution. Time and frequency resolutionare governed by the choice of analysis window and greaterconcentration in one domain is accompanied by greatersmearing in the other.

A time-frequency representation having improved resolution,relative to the spectrogram, is the Wigner-Ville distribution, which may be interpreted as a short-timeFourier transform with a window function that is perfectlymatched to the signal. The Wigner-Ville distribution ishighly-concentrated in time and frequency, but it is alsohighly nonlinear and non-local. Consequently, thisdistribution is very sensitive to noise, and generatescross-components that often mask the components of interest,making it difficult to extract useful information concerningthe distribution of energy in multi-component signals.

Cohen's class ofbilinear time-frequency representations is a class of"smoothed" Wigner-Ville distributions, employing a smoothingkernel that can reduce sensitivity of the distribution tonoise and suppresses cross-components, at the expense ofsmearing the distribution in time and frequency. Thissmearing causes the distribution to be non-zero in regionswhere the true Wigner-Ville distribution shows no energy.

The spectrogram is a member of Cohen's class. It is asmoothed Wigner-Ville distribution with the smoothing kernelequal to the Wigner-Ville distribution of the analysiswindow. The method of reassignment smoothes the Wigner-Villedistribution, but then refocuses the distribution back tothe true regions of support of the signal components. Themethod has been shown to reduce time and frequency smearingof any member of Cohen's class F. Auger and P. Flandrin, "Improving the readability of time-frequency and time-scale representations by the reassignment method", IEEE Transactions on Signal Processing, vol. 43, pp. 1068 – 1089, May 1995.] [P. Flandrin, F. Auger, and E. Chassande-Mottin, "Time-frequency reassignment: From principles to algorithms", in Applications in Time-Frequency Signal Processing (A. Papandreou-Suppappola, ed.), ch. 5, pp. 179 – 203, CRC Press, 2003.] In the case of the reassignedspectrogram, the short-time phase spectrum is used tocorrect the nominal time and frequency coordinates of thespectral data, and map it back nearer to the true regions ofsupport of the analyzed signal.

The Method of Reassignment

Pioneering work on the method of reassignment was firstpublished by Kodera, Gendrin, and de Villedary under thename of "Modified Moving Window Method" [K. Kodera, R. Gendrin, and C. de Villedary, "Analysis of time-varying signals with small BT values", IEEE Transactions on Acoustics, Speech and Signal Processing, vol. ASSP-26, pp. 64 – 76, Feb. 1978.] Their technique enhances the resolution in time andfrequency of the classical Moving Window Method (equivalentto the spectrogram) by assigning to each data point a newtime-frequency coordinate that better-reflects thedistribution of energy in the analyzed signal.

In the classical moving window method, a time-domainsignal, $x(t)$ is decomposed into a set ofcoefficients, $epsilon(\; t,\; omega\; )$, based on a set of elementary signals, $h\_\{omega\}(t)$,defined

$h\_\{omega\}(t)\; =\; h(t)\; e^\{j\; omega\; t\}$

where $h(t)$ is a (real-valued) lowpass kernelfunction, like the window function in the short-time Fouriertransform. The coefficients in this decomposition are defined

where $M\_\{t\}(omega)$ is the magnitude, and$phi\_\{\; au\}(omega)$ the phase, of$X\_\{t\}(omega)$, the Fourier transform of thesignal $x(t)$ shifted in time by $t$and windowed by $h(t)$.

$x(t)$ can be reconstructed from the moving window coefficients by

For signals having magnitude spectra,$M(t,omega)$, whose time variation is slowrelative to the phase variation, the maximum contribution tothe reconstruction integral comes from the vicinity of thepoint $t,omega$ satisfying the phasestationarity condition

or equivalently, around the point $hat\{t\},\; hat\{omega\}$ defined by

This phenomenon is known in such fields as optics as the
principle of stationary phase, which states that for periodic or quasi-periodicsignals, the variation of the Fourier phase spectrum notattributable to periodic oscillation is slow with respect totime in the vicinity of the frequency of oscillation, and insurrounding regions the variation is relatively rapid.Analogously, for impulsive signals, that are concentrated intime, the variation of the phase spectrum is slow withrespect to frequency near the time of the impulse, and insurrounding regions the variation is relatively rapid.

In reconstruction, positive and negative contributions tothe synthesized waveform cancel, due to destructiveinterference, in frequency regions of rapid phase variation.Only regions of slow phase variation (stationary phase) willcontribute significantly to the reconstruction, and themaximum contribution (center of gravity) occurs at the pointwhere the phase is changing most slowly with respect to timeand frequency.

The time-frequency coordinates thus computed are equal to the local group delay, $hat\{t\}\_\{g\}(t,omega)$,and local instantaneous frequency, $hat\{omega\}\_\{i\}(t,omega)$, and are computed from the phase ofthe short-time Fourier transform, which is normally ignoredwhen constructing the spectrogram. These quantities are"local" in the sense that they are represent a windowedand filtered signal that is localized in time and frequency,and are not global properties of the signal under analysis.

The modified moving window method, or method ofreassignment, changes (reassigns) the point of attributionof $epsilon(t,omega)$ to this point of maximumcontribution $hat\{t\}(t,omega),hat\{omega\}(t,omega)$, rather than to the point$t,omega$ at which it is computed. This point issometimes called the "center of gravity" of thedistribution, by way of analogy to a mass distribution. Thisanalogy is a useful reminder that the attribution ofspectral energy to the center of gravity of its distributiononly makes sense when there is energy to attribute, so themethod of reassignment has no meaning at points where thespectrogram is zero-valued.

Efficient Computation of Reassigned Times and Frequencies

In digital signal processing, it is most common to samplethe time and frequency domains. The discrete Fouriertransform is used to compute samples $X(k)$ ofthe Fourier transform from samples $x(n)$ of atime domain signal. The reassignment operations proposed byKodera "et al." cannot be applied directly to thediscrete short-time Fourier transform data, because partialderivatives cannot be computed directly on data that isdiscrete in time and frequency, and it has been suggestedthat this difficulty has been the primary barrier to wideruse of the method of reassignment.

It is possible to approximate the partial derivatives usingfinite differences. For example, the phase spectrum can beevaluated at two nearby times, and the partial derivativewith respect to time be approximated as the differencebetween the two values divided by the time difference, as in

For sufficiently small values of $Delta\; t$ and$Delta\; omega$, and provided that the phasedifference is appropriately "unwrapped", thisfinite-difference method yields good approximations to thepartial derivatives of phase, because in regions of thespectrum in which the evolution of the phase is dominated byrotation due to sinusoidal oscillation of a single, nearbycomponent, the phase is a linear function.

Independently of Kodera "et al." , Nelson arrived at a similar method forimproving the time-frequency precision of short-timespectral data from partial derivatives of the short-time phasespectrum.D. J. Nelson, "Cross-spectral methods for processing speech", Journal of the Acoustical Society of America, vol. 110, pp. 2575 – 2592, Nov. 2001.] It is easily shown that Nelson's "cross spectral surfaces" compute an approximation of the derivatives thatis equivalent to the finite differences method.

Auger and Flandrin showed that the method of reassignment, proposedin the context of the spectrogram by Kodera "et al.", could be extended to any member of Cohen's class of time-frequency representations by generalizing the reassignment operations to

where $W\_\{x\}(t,omega)$ is the Wigner-Villedistribution of $x(t)$, and$Phi(t,omega)$ is the kernel function thatdefines the distribution. They further described anefficient method for computing the times and frequencies forthe reassigned spectrogram efficiently and accuratelywithout explicitly computing the partial derivatives ofphase.

In the case of the spectrogram, the reassignment operationscan be computed by

where $X(t,omega)$ is the short-time Fouriertransform computed using an analysis window$h(t)$, $X\_\{mathcal\{T\}h\}(t,omega)$is the short-time Fourier transform computed using atime-weighted anlaysis window $h\_\{mathcal\{T(t)\; =\; tcdot\; h(t)$ and$X\_\{mathcal\{D\}h\}(t,omega)$ is the short-timeFourier transform computed using a time-derivative analysiswindow $h\_\{mathcal\{D(t)\; =\; frac\{d\}\{dt\}h(t)$.

Using the auxiliary window functions$h\_\{mathcal\{T(t)$ and$h\_\{mathcal\{D(t)$, the reassignment operationscan be computed at any time-frequency coordinate$t,omega$ from an algebraic combination of threeFourier transforms evaluated at $t,omega$. Sincethe these algorithms operate only on short-time spectraldata evaluated at a single time and frequency, and do notexplicitly compute any derivatives, the reassignedtime-frequency coordinates $hat\{omega\}(t\_\{n\},omega\_\{k\})$ and$hat\{t\}(t\_\{n\},omega\_\{k\})$ can be computed fromthree discrete short-time Fourier transforms evaluated at$t\_\{n\},omega\_\{k\}$. This gives an efficientmethod of computing the reassigned discrete short-timeFourier transform provided only that the $|\; X(t,omega)$
^2 is non-zero. This is not much of a restriction,since the reassignment operation itself implies that thereis some energy to reassign, and has no meaning when thedistribution is zero-valued.

=Separability=

The short-time Fourier transform can often be used toestimate the amplitudes and phases of the individualcomponents in a "multi-component" signal, such as aquasi-harmonic musical instrument tone. Moreover, the timeand frequency reassignment operations can be used to sharpenthe representation by attributing the spectral energyreported by the short-time Fourier transform to the pointthat is the local center of gravity of the complex energydistribution.

For a signal consisting of a single component, theinstantaneous frequency can be estimated from the partialderivatives of phase of any short-time Fourier transformchannel that passes the component. If the signal is to bedecomposed into many components,

$x(t)\; =\; sum\_\{n\}\; A\_\{n\}(t)\; e^\{j\; heta\_\{n\}(t)\}$

and the instantaneous frequency of each component is defined as the derivative of its phase with respect to time, that is,

$omega\_\{n\}(t)\; =\; frac\{d\; heta\_\{n\}(t)\}\{d\; t\},$

then the instantaneous frequency of each individual component can be computed from the phase of the response of a filter that passesthat component, provided that no more than one component lies in the passband of the filter.

This is the property, in the frequency domain, that Nelsoncalled "separability" and is required of all signals so analyzed. If this property is not met, thenthe desired multi-component decomposition cannot be achieved,because the parameters of individual components cannot beestimated from the short-time Fourier transform. In suchcases, a different analysis window must be chosen so thatthe separability criterion is satisfied.

If the components of a signal are separable in frequencywith respect to a particular short-time spectral analysiswindow, then the output of each short-time Fourier transformfilter is a filtered version of, at most, a singledominant (having significant energy) component, and so thederivative, with respect to time, of the phase of the$X(t,omega\_\{0\})$ is equal to the derivative withrespect to time, of the phase of the dominant component at$omega\_\{0\}$. Therefore, if a component,$x\_\{n\}(t)$, having instantaneous frequency$omega\_\{n\}(t)$ is the dominant component in thevicinity of $omega\_\{0\}$, then the instantaneousfrequency of that component can be computed from the phaseof the short-time Fourier transform evaluated at$omega\_\{0\}$. That is,

Thus, the partial derivative with respect to time of thephase of the short-time Fourier transform can be used tocompute the instantaneous frequencies of the individualcomponents in a multi-component signal, provided only thatthe components are separable in frequency by the chosenanalysis window.

---

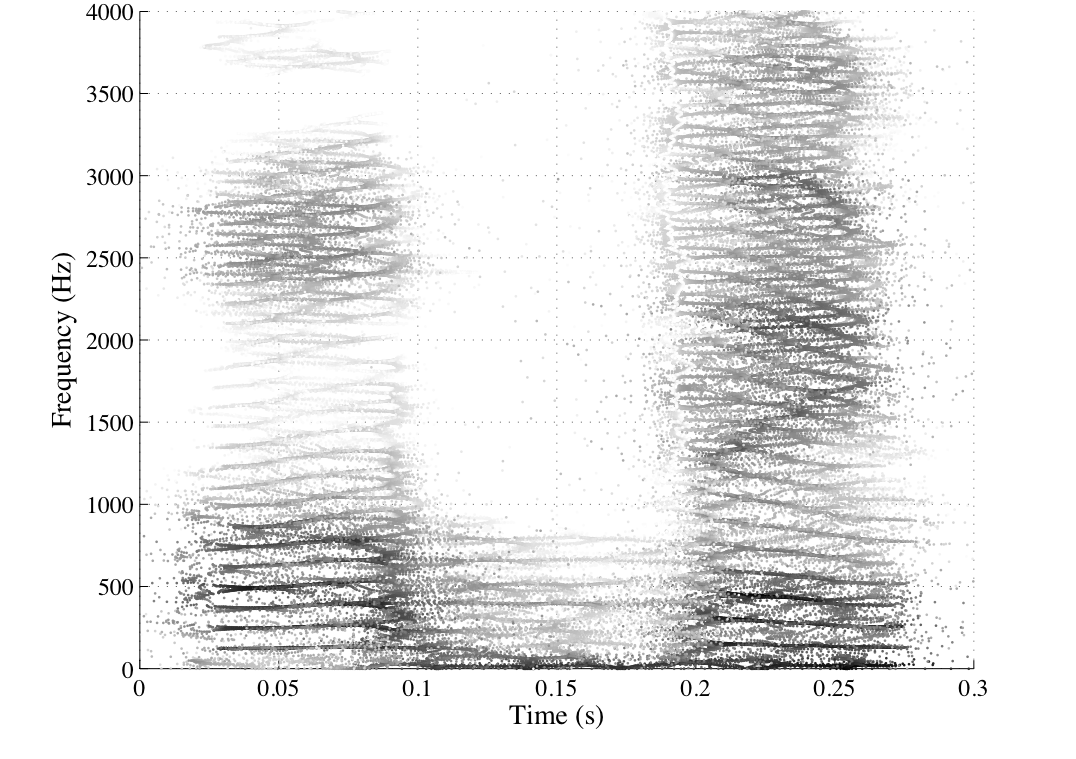
thumb|400px">
Long-window reassigned spectrogram of the word "open",computed using a 54.4 ms Kaiser window with a shaping parameter of 9, emphasizing harmonics.

thumb|400px">
Short-window reassigned spectrogram of the word "open",computed using a 13.6 ms Kaiser window with a shaping parameter of 9, emphasizing formants and glottal pulses.

Just as each bandpass filter in the short-time Fouriertransform filterbank may pass at most a single complexexponential component, two temporal events must besufficiently separated in time that they do not lie in thesame windowed segment of the input signal. This is theproperty of separability in the time domain, and isequivalent to requiring that the time between two events begreater than the length of the impulse response of theshort-time Fourier transform filters, the span of non-zerosamples in $h(t)$.

Separability in time and in frequency is required ofcomponents to be resolved in a reassigned time-frequencyrepresentation. If the components in a decomposition areseparable in a certain time-frequencyrepresentation, then the components can be resolved by thattime-frequency representation, and using the method ofreassignment, can be characterized with much greaterprecision than is possible using classical methods.

In general, there are an infinite number of equally-validdecompositions for a multi-component signal.The separability property must be considered in the context of the desired decomposition. For example, in the analysis of a speech signal,an analysis window that is long relative to the time between glottal pulsesis sufficient to separate harmonics, but the individual glottal pulses will be smeared, becausemany pulses are covered by each window(that is, the individual pulses are not separable, in time,by the chosen analysis window). An analysis window that is much shorter than thetime between glottal pulses may resolve the glottal pulses, because no window spansmore than one pulse, but the harmonic frequenciesare smeared together, because the main lobe of the analysis windowspectrum is wider than the spacing between the harmonics(that is, the harmonics are not separable, in frequency,by the chosen analysis window).

References

Further reading

*S. A. Fulop and K. Fitz, "A spectrogram for the twenty-first century", Acoustics Today, vol. 2, no. 3, pp. 26–33, 2006.
*S. A. Fulop and K. Fitz, "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications", Journal of the Acoustical Society of America, vol. 119, pp. 360 – 371, Jan 2006.

External links

* [http://tftb.nongnu.org/ TFTB — Time-Frequency ToolBox]
* [http://www.klingbeil.com/spear/ SPEAR - Sinusoidal Partial Editing Analysis and Resynthesis]
* [http://www.cerlsoundgroup.org/Loris/ Loris - Open-source software for sound modeling and morphing]
* [http://musicalgorithms.ewu.edu/algorithms/roughness.html SRA - A web-based research tool for spectral and roughness analysis of sound signals] (supported by a Northwest Academic Computing Consortium grant to J. Middleton, Eastern Washington University)