Kautz graph

right|frame">
Sample of K. graph with M=2: on the left N=1, on the right N=2.The edges of the left graph correspond to the nodes of right graph.

The Kautz graph $K\_M^\{N\; +\; 1\}$ is a
directed graph of degree $M$ and dimension $N+1$, which has $(M\; +1)M^\{N\}$ vertices labeled by allpossible strings $s\_0\; cdots\; s\_N$ of length $N\; +1$ which are composed of characters $s\_i$ chosen froman alphabet $A$ containing $M\; +\; 1$ distinctsymbols, subject to the condition that adjacent characters in thestring cannot be equal ($s\_i\; eq\; s\_\{i+\; 1\}$).

The Kautz graph $K\_M^\{N\; +\; 1\}$ has $(M\; +\; 1)M^\{N+\; 1\}$ edges

$\{(s\_0\; s\_1\; cdots\; s\_N,s\_1\; s\_2\; cdots\; s\_N\; s\_\{N\; +\; 1\})|\; ;\; s\_i\; in\; A\; ;\; s\_i\; eq\; s\_\{i\; +\; 1\}\; \}\; ,$

It is natural to label each such edge of $K\_M^\{N\; +\; 1\}$as $s\_0s\_1\; cdots\; s\_\{N\; +\; 1\}$, giving a one-to-one correspondencebetween edges of the Kautz graph $K\_M^\{N\; +\; 1\}$and vertices of the Kautz graph$K\_M^\{N\; +\; 2\}$.

Kautz graphs are closely related to De Bruijn graphs.

Properties

* For a fixed degree $M$ and number of vertices $V\; =\; (M\; +\; 1)\; M^N$, the Kautz graph has the smallest diameter of any possible directed graph with $V$ vertices and degree $M$.

* All Kautz graphs have Eulerian cycles. (An Eulerian cycle is one which visits each edge exactly once-- This result follows because Kautz graphs have in-degree equal to out-degree for each node)

* All Kautz graphs have a Hamiltonian cycle (This result follows from the correspondence described above between edges of the Kautz graph $K\_M^\{N\}$ and vertices of the Kautz graph $K\_M^\{N\; +\; 1\}$; a Hamiltonian cycle on $K\_M^\{N\; +\; 1\}$ is given by an Eulerian cycle on $K\_M^\{N\}$)

* A degree-$k$ Kautz graph has $k$ disjoint paths from any node $x$ to any other node $y$. This property is violated by the graph ( [http://en.wikipedia.org/wiki/
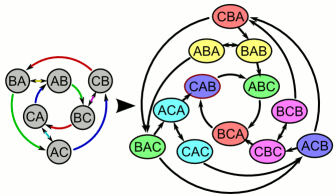] above right) incorrectly supplied as an example of a $K\_2^2$ graph.

In computing

The Kautz graph has been used as a network topology for connecting processors in high-performance computing [cite web | url=http://pl.atyp.us/wordpress/?p=1275 | title=The Kautz Graph | author=Darcy, Jeff | date=2007-12-31 | publisher= [http://pl.atyp.us/wordpress/ Canned Platypus] ] and fault-tolerant computing [cite conference |first=Dongsheng |last=Li |coauthors=Xicheng Lu, Jinshu Su |title=Graph-Theoretic Analysis of Kautz Topology and DHT Schemes |booktitle=Network and Parallel Computing: IFIP International Conference |pages=308-315 |publisher=NPC |date=2004 |location=Wuhan, China |url=http://books.google.com/books?id=DpDwhffRCjwC&pg=PA308&lpg=PA308&dq=kautz+graph&source=web&ots=QWy7s3YiHU&sig=KHsfzBYxBWdiNjZ4pn8YUoArB0A&hl=en |accessdate=2008-03-05 | isbn=3540233881 ] applications: such a network is known as a Kautz network.

Notes