Brillouin and Langevin functions

=Brillouin Function=

The Brillouin functionC. Kittel, "Introduction to Solid State Physics" (8th ed.), pages 303-4] [Citation
last = Darby
first = M.I.
author-link =
last2 =
first2 =
author2-link =
title = Tables of the Brillouin function and of the related function for the spontaneous magnetization
journal = Brit. J. Appl. Phys.
volume = 18
issue =
pages = 1415-1417
date =
year = 1967
url =
doi =
id = ] is a special function defined by the following equation:

:$B\_J(x)\; =\; frac\{2J\; +\; 1\}\{2J\}\; coth\; left\; (\; frac\{2J\; +\; 1\}\{2J\}\; x\; ight\; )\; -\; frac\{1\}\{2J\}\; coth\; left\; (\; frac\{1\}\{2J\}\; x\; ight\; )$

The function is usually applied (see below) in the context where "x" is a real variable and "J" is a positive integer or half-integer. In this case, the function varies from -1 to 1, approaching +1 as "x" approaches +∞ and -1 as "x" approaches -∞.

The function is best known for arising in the calculation of the magnetization of an ideal paramagnet. In particular, it describes the dependency of the magnetization $M$ on the applied magnetic field $B$ and the total angular momentum quantum number J of the microscopic magnetic moments of the material. The magnetization is given by::$M\; =\; N\; g\; mu\_B\; J\; cdot\; B\_J(x)$

where
*$N$ is the number of atoms per unit volume,
*$g$ the g-factor,
*$mu\_B$ the Bohr magneton,
*$x$ is the ratio of the Zeeman energy of the magnetic moment in the external field to the thermal energy $k\_B\; T$:::$x\; =\; frac\{g\; mu\_B\; J\; B\}\{k\_B\; T\}$
*$k\_B$ is the Boltzmann constant and $T$ the temperature.

:

Langevin Function

---

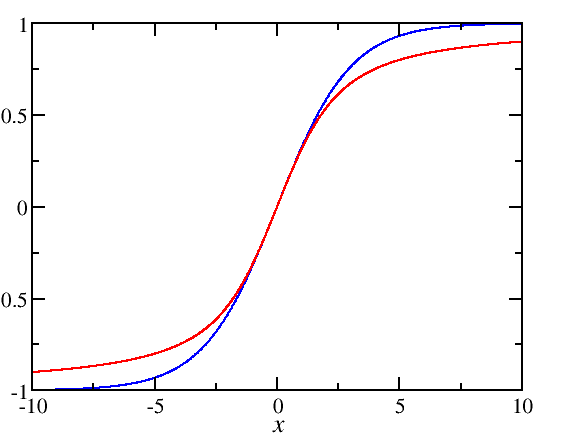
thumb|right|Langevin function (red line), compared with">$tanh(x/3)$ (blue line).

In the classical limit, the moments can be continuously aligned in the field and $J$ can assume all values ($J\; o\; infty$). The Brillouin function is then simplified into the Langevin function, named after Paul Langevin:

:$L(x)\; =\; coth(x)\; -\; frac\{1\}\{x\}$

High Temperature Limit

When i.e. when $mu\_B\; B\; /\; k\_B\; T$ is small, the expression of the magnetization can be approximated by the Curie's law:

:$M\; =\; C\; cdot\; frac\{H\}\{T\}$

where $C\; =\; frac\{N\; g^2\; J(J+1)\; mu\_B^2\}\{3k\_B\}$ is a constant. One can note that $gsqrt\{J(J+1)\}$ is the effective number of Bohr magnetons.

High Field Limit

When $x\; oinfty$, the Brillouin function goes to 1. The magnetization saturates with the magnetic moments completely aligned with the applied field:

:$M\; =\; N\; g\; mu\_B\; J$

References