Disjoining pressure

Disjoining pressure (symbol Π_d), in surface chemistry, according to an IUPAC definition^[1], arises from an attractive interaction between two surfaces. For two flat and parallel surfaces, the value of the disjoining pressure (i.e., the force per unit area) can be calculated as the derivative of the Gibbs energy of interaction per unit area in respect to distance (in the direction normal to that of the interacting surfaces). There is also a related concept of disjoining force, which can be viewed as disjoining pressure times the surface area of the interacting surfaces.

The concept of disjoining pressure has been introduced by Derjaguin (1936) as the difference between the pressure in a region of a phase adjacent to a surface confining it, and the pressure in the bulk of this phase^[2].

Description

Disjoining pressure can be expressed as^[3]:

$\Pi_D = - {1 \over A} \left( \frac{\partial G}{\partial x} \right)_{T,V, A}$

where:

• Π_d - disjoining pressure, N/m²
• A - the surface area of the interacting surfaces, m²
• G - total Gibbs energy of the interaction of the two surfaces, J
• x - distance, m
• indices T, V and A signify that the temperature, volume, and the surface area remain constant in the derivative.

Dependence of the pressure in the film at surface A and the pressure in the bulk

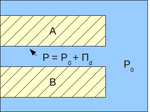
Using the concept of the disjoining pressure, the pressure in a film can be viewed as^[3]:

P = P₀ + Π_D

where:

• P - pressure in a film, Pa
• P₀ - pressure in the bulk of the same phase as that of the film, Pa.

Disjoining pressure is interpreted as a sum of several interactions: dispersion forces, electrostatic forces between charged surfaces, interactions due to layers of neutral molecules adsorbed on the two surfaces, and the structural effects of the solvent.

See also

• Capillary condensation
• Capillary pressure

References

1. ^ "Disjoining pressure". Entry in the IUPAC Compendium of Chemical Terminology ("The Gold Book"), the International Union of Pure and Applied Chemistry, 2nd edition, 1997
2. ^ A. Adamson, A. Gast, "Physical Chemistry of Surfaces", 6th edition, John Wiley and Sons Inc., 1997, page 247.
3. ^ ^{a b} Hans-Jürgen Butt, Karlheinz Graf, Michael Kappl,"Physics and chemistry of interfaces", John Wiley & Sons Canada, Ltd., 1 edition, 2003, page 95 (Google books)