Directed acyclic word graph

For the US Department of Defense review panel, see Deputy’s Advisory Working Group.

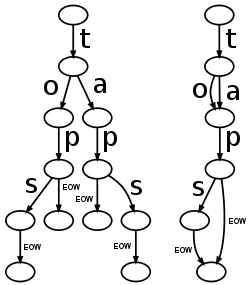The strings "tap", "taps", "top", and "tops" stored in a Trie (left) and a DAWG (right), EOW stands for End-of-word.

In computer science, a directed acyclic word graph (sometimes abbreviated as DAWG) is a data structure that represents a set of strings, and allows for a query operation that tests whether a given string belongs to the set in time proportional to its length. In these respects, a DAWG is very similar to a trie, but it is much more space efficient.

A DAWG is represented as a directed acyclic graph with a single source vertex (a vertex with no incoming edges), in which each edge of the graph is labeled by a letter, symbol, or special end-of-string marker, and in which each vertex has at most one outgoing edge for each possible letter or symbol. The strings represented by the DAWG are formed by the symbols on paths in the DAWG from the source vertex to any sink vertex (a vertex with no outgoing edges). A DAWG can also be interpreted as an acyclic finite automaton that accepts the words that are stored in the DAWG.

Thus, a trie (a rooted tree with the same properties of having edges labeled by symbols and strings formed by root-to-leaf paths) is a special kind of DAWG. However, by allowing the same vertices to be reached by multiple paths, a DAWG may use significantly fewer vertices than a trie. Consider, for example, the four English words "tap", "taps", "top", and "tops". A trie for those four words would have 11 vertices, one for each of the strings formed as a prefix of one of these words, or for one of the words followed by the end-of-string marker. However, a DAWG can represent these same four words using only six vertices v_i for 0 ≤ i ≤ 5, and the following edges: an edge from v₀ to v₁ labeled "t", two edges from v₁ to v₂ labeled "a" and "o", an edge from v₂ to v₃ labeled "p", an edge v₃ to v₄ labeled "s", and edges from v₃ and v₄ to v₅ labeled with the end-of-string marker.

The primary difference between DAWG and trie is the elimination of suffix redundancy in storing strings. The trie eliminates prefix redundancy since all common prefixes are shared between strings, such as between doctors and doctorate the doctor prefix is shared. In a DAWG common suffixes are also shared, such as between desertion and destruction both the prefix des- and suffix -tion are shared. For dictionary sets of common English words, this translates into major memory usage reduction.

Because the terminal nodes of a DAWG can be reached by multiple paths, a DAWG cannot directly store auxiliary information relating to each path, e.g. a word's frequency in the English language. However, if at each node we store a count of the number of unique paths through the structure from that point, we can use it to retrieve the index of a word, or a word given its index.^[1] The auxiliary information can then be stored in an array.

See also

• GADDAG

References

1. ^ Kowaltowski, T.; CL. Lucchesi (1993), "Applications of finite automata representing large vocabularies", Software-Practice and Experience 1993: 15–30, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.56.5272&rep=rep1&type=pdf. 

• Appel, Andrew; Jacobsen, Guy (1988), possibly first mention of the data structure, "The World's Fastest Scrabble Program" (PDF), Communications of the ACM, http://www.cs.cmu.edu/afs/cs/academic/class/15451-s06/www/lectures/scrabble.pdf .
• Crochemore, Maxime; Vérin, Renaud (1997), "Direct construction of compact directed acyclic word graphs", Combinatorial Pattern Matching, Lecture Notes in Computer Science, Springer-Verlag, pp. 116–129, doi:10.1007/3-540-63220-4_55 .
• Inenaga, S.; Hoshino, H.; Shinohara, A.; Takeda, M.; Arikawa, S. (2001), "On-line construction of symmetric compact directed acyclic word graphs", Proc. 8th Int. Symp. String Processing and Information Retrieval, 2001. SPIRE 2001, pp. 96–110, doi:10.1109/SPIRE.2001.989743, ISBN 0-7695-1192-9, http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=989743 .
• Jansen, Cees J. A.; Boekee, Dick E. (1990), "On the significance of the directed acyclic word graph in cryptology", Advances in Cryptology — AUSCRYPT '90, Lecture Notes in Computer Science, 453, Springer-Verlag, pp. 318–326, doi:10.1007/BFb0030372, ISBN 3-540-53000-2 .

External links

• National Institute of Standards and Technology
• DAWG implementation in C# by Samuel Allen
• Optimal DAWG Creation Step By Step Treatment
• Documentation for The World's Most Powerful DAWG Encoding: Caroline Word Graph